Problema
(Indicado a partir do 7º ano do E. F.)
A partir de uma folha de papel quadrada de [tex]10 \, \text{cm}[/tex] de lado, é possível cortar vários círculos tais que a soma dos seus diâmetros seja 5 metros ou mais?
Justifique.
Adaptado do livro Um Círculo Matemático de Moscou, de Sergey Dorichenko.
Solução
I – Divida cada lado do quadrado em segmentos de [tex]0,2\, \text{cm}[/tex] cada e trace retas paralelas aos lados de modo a obter uma malha, conforme mostra a figura abaixo.
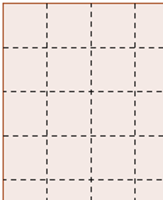
Dentro de cada quadradinho trace uma circunferência tangenciando os seus lados, conforme mostra a figura abaixo.
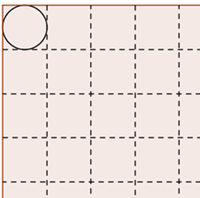
Observe que cada lado do quadrado foi dividido em [tex]50[/tex] segmentos de [tex]0,2\, \text{cm}[/tex] cada; assim, a partir do quadrado, obtivemos [tex]50\times50=2\,500[/tex] quadradinhos e, consequentemente, [tex]2\,500[/tex] círculos com diâmetros de [tex]0,2\, \text{cm}[/tex].
Somando todos os diâmetros vamos, então, obter:
[tex]\quad \quad S=\underbrace{0,2+0,2+\cdots+0,2}_{2500\, vezes}=2500\times0,2=500\, \text{cm}[/tex],
ou seja, [tex]S=5\, \text{m}[/tex].
II – Para obtermos um valor de [tex]S[/tex] maior, basta diminuirmos o comprimento dos segmentos de [tex]0,2\, \text{cm}[/tex].
Por exemplo, com segmentos de [tex]0,1\, \text{cm}[/tex], obteríamos [tex]10\,000[/tex] círculos de diâmetros [tex]0,1\, \text{cm}[/tex] e nesse caso:
[tex]\quad \quad S=\underbrace{0,1+0,1+\cdots+0,1}_{10\,000\, vezes}=10\,000\times0,1=1\,000\, \text{cm}[/tex],
ou seja, teríamos [tex]\, S=10\, \text{m}[/tex].
Solução elaborada pelos Moderadores do Blog.
