.Problema para ajudar na escola: O dilema de um feirante

Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)

---

Um feirante deseja comprar um total de não mais que [tex]50[/tex] quilos de um determinado produto.
Se Pedro e Joaquim são os únicos fornecedores do produto na região, estabeleça um sistema de desigualdades que descreva todas as possíveis combinações, não necessariamente inteiras, de quilogramas que podem ser compradas de cada fornecedor.
Esboce a solução em um plano cartesiano.

Solução

---

Sejam [tex]x\, [/tex] e [tex]\, y[/tex] números reais que representam as quantidades de quilogramas a serem compradas dos fornecedores Pedro e Joaquim, respectivamente.
Dessa forma, as informações matemáticas que podemos extrair do enunciado são estas:

• [tex] x \geqslant 0[/tex],
• [tex] y \geqslant 0[/tex],
• [tex] x+y \leqslant 50[/tex] ,

e o sistema de desigualdades que descreve todas as possíveis combinações de compra do feirante é este:

[tex] \begin{cases}\, x \geqslant 0\\
\, y \geqslant 0\\
\, x+y \leqslant 50 \end{cases}\, \, .[/tex]

Um sistema formado por essas desigualdades e com soluções não necessariamente inteiras só pode ser solucionado graficamente. Vejamos, portanto, como fica a solução desse sistema de desigualdades em um plano cartesiano [tex]xOy.[/tex]
A solução desse sistema são os pontos [tex]P=(x,y)[/tex] do plano cartesiano que satisfazem simultaneamente às seguintes condições:

[tex]\boxed{x \geqslant 0}\qquad[/tex] ; [tex]\qquad \boxed{y \geqslant 0}\qquad [/tex] ; [tex]\qquad \boxed{x+y \leqslant 50}[/tex] ,

assim, vamos estudar cada uma dessas condições isoladamente para depois analisarmos as três simultaneamente.

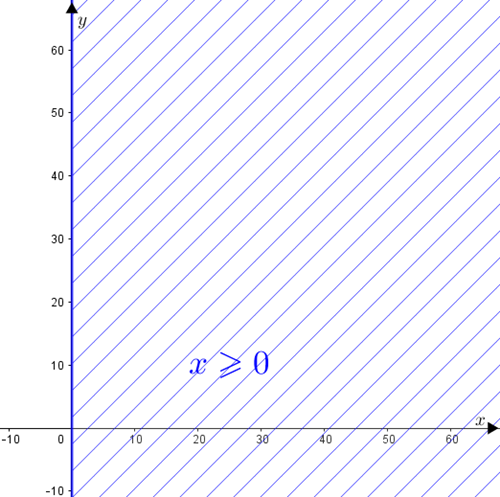
• [tex]x \geqslant 0[/tex]
  Os pontos [tex]P=(x,y)[/tex] que satisfazem esta condição são:
  – aqueles que estão sobre o eixo [tex]y[/tex] ([tex]x=0[/tex]),
  – aqueles que estão à direita do eixo [tex]y[/tex] ([tex]x \gt 0[/tex]).

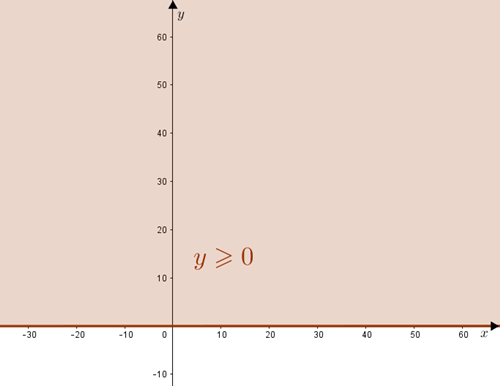
• [tex]y \geqslant 0[/tex]
  Os pontos [tex]P=(x,y)[/tex] que satisfazem esta condição são:
  – aqueles que estão sobre o eixo [tex]x[/tex] ([tex]y=0[/tex]),
  – aqueles que estão acima do eixo [tex]x[/tex] ([tex]y \gt 0[/tex]).

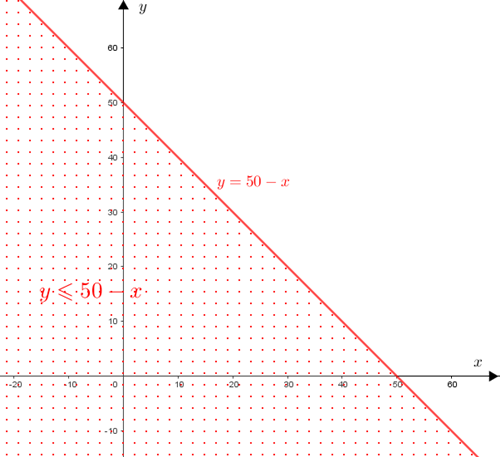
• [tex]x+y \leqslant 50[/tex]
  Os pontos [tex]P=(x,y)[/tex] que satisfazem esta condição são:
  – aqueles que estão sobre a reta [tex]y=50-x[/tex],
  – aqueles que estão abaixo da reta [tex]y=50-x[/tex] ([tex]x+y \lt 50[/tex]).

Fazendo a interseção das três regiões acima, obtemos, finalmente, a solução do sistema em questão.

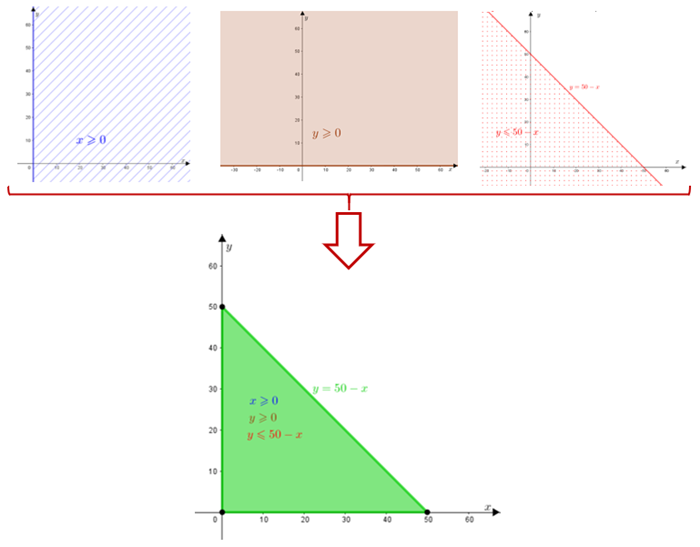
Assim, a região que representa todas as opções possíveis de compra do produto pelo feirante é a região definida pelo triângulo retângulo determinado pelos eixos [tex]Ox[/tex] e [tex]Oy[/tex] e pela reta [tex]y=50-x[/tex], cujos vértices são os pontos [tex](0,0),(50,0),(0,50).[/tex]

---

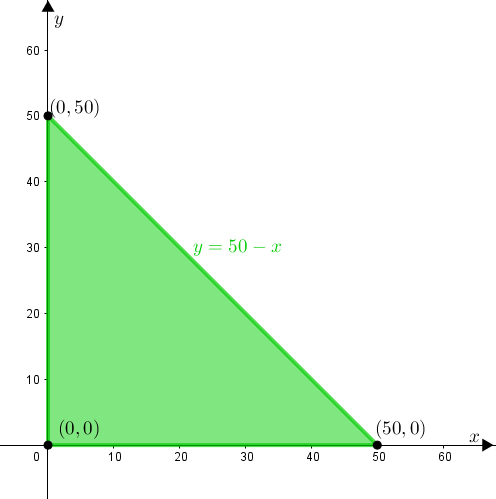
Solução elaborada pelos Moderadores do Blog.