Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
Informalmente:
- Oferta é a quantidade de um produto ou serviço disponível para compra.
- Demanda é a quantidade de produtos ou serviços que os consumidores estão dispostos a comprar.
Quando a demanda é maior do que a oferta, os preços dos produtos tendem a subir, já que os consumidores se dispõem a pagar mais para obter um determinado item. Por outro lado, quando a oferta é maior do que a demanda, os preços tendem a cair.
Matematicamente duas funções são associadas a esses processos: a função demanda e a função oferta.
- Função demanda: relaciona a quantidade demandada como função do preço de um bem.
- Função oferta: relaciona a quantidade ofertada como função do preço de um bem.
O preço que iguala a quantidade ofertada e a quantidade demandada de um bem é denominado preço de equilíbrio.
Suponha que as equações de oferta e demanda de um certo produto são, respectivamente:
[tex]\qquad \qquad 3q_o-220p+1800=0 \qquad \textcolor{#800000}{(o)} [/tex]
[tex]\qquad \qquad 3q_d+100p-1800=0 \qquad \textcolor{#800000}{(d)} [/tex]
nas quais [tex]p[/tex] representa o preço por unidade, em reais, e [tex]q_o, \, q_d[/tex] representam respectivamente as quantidades de oferta e demanda em uma semana.
Nessas condições:
(a) Encontre algebricamente o preço de equilíbrio do produto, no período.
(b) Interprete graficamente esse preço de equilíbrio.
Solução
(a) Seja [tex]p_e[/tex] o preço de equilíbrio do produto, no período. Como o preço de equilíbrio é o preço que iguala a quantidade ofertada e a quantidade demandada desse produto no período, seja [tex]q[/tex] essa quantidade.
Por [tex]\textcolor{#800000}{(o)} \, [/tex] e [tex] \, \textcolor{#800000}{(d)} \, [/tex], segue que:
[tex]\qquad \qquad 3q-220p_e+1800=0[/tex]
[tex]\qquad \qquad 3q+100p_e-1800=0 [/tex]
e, portanto,
[tex]\qquad \cancel{3q}-220p_e+1800=\cancel{3q}+100p_e-1800[/tex]
[tex]\qquad 1800+1800=100p_e+220p_e[/tex]
[tex]\qquad 3600=320p_e[/tex]
[tex]\qquad p_e=11,25 \, .[/tex]
Assim, o preço de equilíbrio do produto no período é [tex] \, \fcolorbox{black}{#eee0e5}{$R\$ \, 11,25$} \, [/tex] e esse preço corresponde à seguinte quantidade [tex]q[/tex] do produto:
[tex]\qquad 3q+100p_e-1800=0 [/tex]
[tex]\qquad 3q+100\times 11,25-1800=0 [/tex]
[tex]\qquad 3q+ 1125-1800=0 [/tex]
[tex]\qquad 3q=675 [/tex]
[tex]\qquad q=225[/tex] unidades.
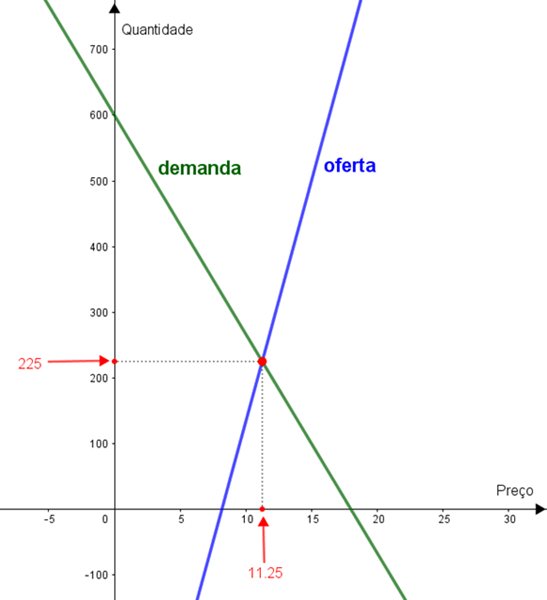
(b) Em um plano cartesiano, as equações [tex]\textcolor{#800000}{(o)} \, [/tex] e [tex] \, \textcolor{#800000}{(d)} \, [/tex] definem duas retas não paralelas.
Particularmente, o ponto de interseção dessas retas tem como coordenadas o preço de equilíbrio e a respectiva quantidade ofertada/demandada do produto no período.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
