✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 9º ano do E. F.)
Encontre as medidas dos catetos de um triângulo retângulo sabendo que sua hipotenusa tem comprimento de [tex]13[/tex] metros e um dos catetos tem comprimento [tex]7[/tex] metros maior do que o outro.
Solução
Se [tex]x[/tex] metros for a medida de um dos catetos então o outro cateto medirá [tex]x+7[/tex] metros, conforme ilustra a figura abaixo.
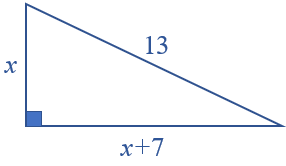
Como a hipotenusa tem comprimento de [tex]13[/tex] metros, aplicando o Teorema de Pitágoras, segue que:
[tex]\qquad x^2+(x+7)^2=13^2[/tex]
[tex]\qquad x^2+x^2+14x+49=169[/tex]
[tex]\qquad 2x^2+14x-120=0[/tex]
[tex]\qquad \boxed{x^2+7x-60=0} \, .[/tex]
Resolvendo esta equação do segundo grau encontramos as raízes [tex]x_1=5[/tex] e [tex]x_2=-12[/tex], sendo que a segunda raiz deve ser descartada, pois as medidas dos lados de um triângulo são sempre positivas.
Portanto, os catetos do triângulo em questão medem [tex] \, \fcolorbox{black}{#c0cef9}{$\text{5 metros e 12 metros}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Participou da discussão o Clube OCTETO MATEMÁTICO.