Problema
(Indicado a partir do 9º ano do E. F.)
Duas peças circulares se sobrepõem como mostrado na figura.
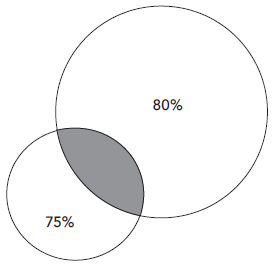
A região não sobreposta da peça menor corresponde a [tex]75\%[/tex] de sua área e a região não sobreposta da peça maior corresponde a [tex]80\%[/tex] de sua área.
Calcule a razão entre o raio da peça maior e o raio da peça menor.
Solução
Sejam [tex]R[/tex] e [tex]r[/tex] os raios das peças maior e menor, respectivamente.
Observe na próxima figura que [tex]25\%[/tex] da área da menor corresponde a [tex]20\%[/tex] da área da maior.
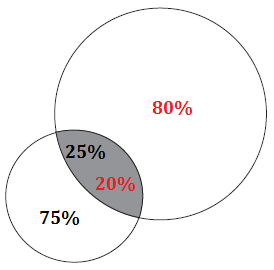
Portanto, [tex]\dfrac{25}{100}\cdot \pi \cdot r^2=\dfrac{20}{100}\cdot \pi \cdot R^2[/tex], ou seja, [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{R}{r}=\dfrac{\sqrt{5}}{2}$}[/tex].
Solução elaborada pelos Moderadores do Blog.
