✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
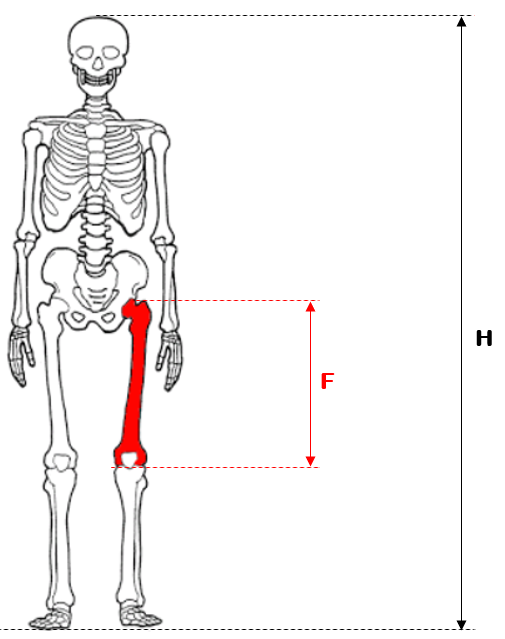
(UFPE-1979) A altura [tex]H[/tex] de um homem varia com o tamanho [tex]F[/tex] do seu fêmur, de acordo com a seguinte fórmula:
[tex]\qquad \qquad H = 69, 089 + 2, 238 F\, [/tex] (medidas expressas em [tex]\text{cm}[/tex]).
Se a idade ultrapassa [tex]30[/tex] anos, subtrai-se [tex]0,06\, \text{cm}[/tex] por cada ano após os [tex]30[/tex] anos.
Qual a altura estimada de um homem de [tex]40[/tex] anos cujo fêmur mede [tex]40\, \text{cm}[/tex]?
Solução 1
Vamos dividir os nossos cálculos em duas etapas.
- Sabemos que a relação entre a altura [tex]H[/tex] de um homem e o tamanho [tex]F[/tex] do seu fêmur é [tex]\boxed{H = 69, 089 + 2, 238 F\, }\, [/tex], tomando as medidas em centímetros.
Assim, a altura estimada de um homem cujo fêmur mede [tex]40\, \text{cm}[/tex] poderia ser assim calculada:
[tex]\qquad H = 69, 089 + 2, 238 \times 40[/tex]
[tex]\qquad H = 69, 089 + 89,52[/tex]
[tex]\qquad \boxed{H = 158,609\, \text{cm}}\, .[/tex] - Mas, como o homem tem [tex]40[/tex] anos, devemos retirar do [tex]H[/tex] calculado [tex]0,06\, \text{cm}[/tex] por cada ano após os [tex]30[/tex] anos, ou seja, devemos retirar [tex]0,06 \times 10=0,6\, \text{cm}\, [/tex] de [tex]H =158,609\, \text{cm}\, .[/tex]
Portanto, estima-se que a altura de um homem de [tex]40[/tex] anos cujo fêmur mede [tex]40\, \text{cm}[/tex] é [tex]\boxed{158,609-0, 6=158,009\, \text{cm}}\, [/tex], ou seja, aproximadamente [tex]\, \fcolorbox{black}{#eee0e5}{$158\, \text{cm}$}\, [/tex] ou [tex]\, \fcolorbox{black}{#eee0e5}{$1,58\, m$}\, . [/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Podemos definir uma relação geral entre a altura [tex]H[/tex] de um homem e o tamanho [tex]F[/tex] do seu fêmur de uma maneira diferente, mas de modo a obter os mesmos resultados.
Observe:
[tex]\quad H = \begin{cases} 69, 089 + 2, 238 F\, , \text{ se a idade do homem não ultrapassar os 30 anos;} \\
\, \, \\
69, 089 + 2, 238 F-0,06n, \, \begin{align*}&\text{ se a idade do homem ultrapassar os 30 anos,}\\
&\, \text{sendo } n \text{ o número de anos que excede 30.}\end{align*}
\end{cases}\, [/tex]
com as medidas [tex]H\, [/tex] e [tex]\, F[/tex] expressas em centímetros.
A partir dessa relação, vamos estimar a altura de um homem de [tex]40[/tex] anos cujo fêmur mede [tex]40\, \text{cm}[/tex]:
- para isso usaremos a igualdade [tex]H=69, 089 + 2, 238 F -0,06n[/tex], com [tex]F=40\, \text{cm}\, [/tex] e [tex]\, n=10\, .[/tex]
Vejamos:
[tex]\qquad H=69, 089 + 2, 238 F-0,06n[/tex]
[tex]\qquad H=69, 089 + 2, 238 \times 40-0,06\times 10[/tex]
[tex]\qquad H=69, 089 + 89,52-0,6[/tex]
[tex]\qquad H=158,009\, \text{cm}[/tex]
[tex]\qquad H\approx 158\, \text{cm}\, .[/tex]
Portanto, estima-se que a altura de um homem de [tex]40[/tex] anos cujo fêmur mede [tex]40\, \text{cm}[/tex] é, aproximadamente, [tex]\, \fcolorbox{black}{#eee0e5}{$158\, \text{cm}$}\, [/tex] ou [tex]\, \fcolorbox{black}{#eee0e5}{$1,58\, m$}\, . [/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
