✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
Uma circunferência de raio 2 cm está inscrita em um quadrado, e este, por sua vez, está inscrito em outra circunferência, como podemos ver na figura.
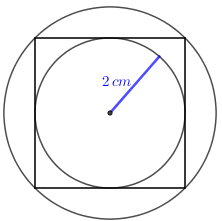
Quantos milímetros mede o raio da circunferência externa?
Solução
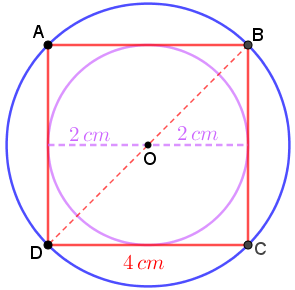
Observe a figura abaixo, na qual visualizamos uma circunferência de raio [tex]2 \, \text{cm}[/tex] inscrita no quadrado [tex]ABCD[/tex] que está inscrito em outra circunferência.
Veja que a medida do raio da circunferência externa é a metade do comprimento da diagonal do quadrado [tex]ABCD \, [/tex] e que, particularmente, a diagonal [tex]\overline{BD}[/tex] é a hipotenusa do triângulo retângulo [tex]BCD \, [/tex], cujos catetos têm como medida o comprimento do lado do quadrado [tex]ABCD[/tex], ou seja, [tex]4 \, \text{cm}.[/tex]
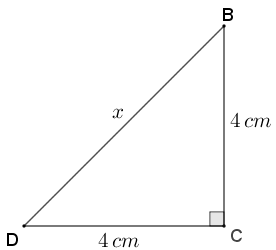
Seja, então, [tex]x[/tex] o comprimento em centímetros do segmento [tex]\overline{BD}[/tex].
Pelo Teorema de Pitágoras, segue que:
[tex]\qquad x^2=4^2+4^2[/tex]
[tex]\qquad x^2=16+16[/tex]
[tex]\qquad x^2=32[/tex]
[tex]\qquad x^2=2^5[/tex]
e como [tex]x\gt 0[/tex], uma vez que é o comprimento do lado de um triângulo, temos que
[tex]\qquad x=\sqrt{2^5}[/tex]
[tex]\qquad x=2^2 \, \sqrt{2} \, [/tex]
[tex]\qquad x=4 \, \sqrt{2} \, .[/tex]
Portanto, o raio da circunferência externa é [tex]r=\dfrac{4 \, \sqrt{2}}{2} \, \text{cm}[/tex], isto é, [tex]r=2 \, \sqrt{2} \, \text{cm}\, .[/tex]
Para expressar a medida desse raio em milímetros, precisamos lembrar que [tex]1 \, \text{cm}=10 \, \text{mm}\, [/tex] e, assim, [tex]\fcolorbox{black}{#eee0e5}{$r=20 \, \sqrt{2} \, \text{mm}$} \, [/tex] ou [tex] \, \fcolorbox{black}{#eee0e5}{$r\approx 28,28 \, \text{mm}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
