✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
Sejam [tex]x[/tex] e [tex]y[/tex] números reais positivos.
Que produto notável cada figura abaixo sugere?
(a)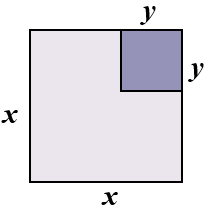
(b)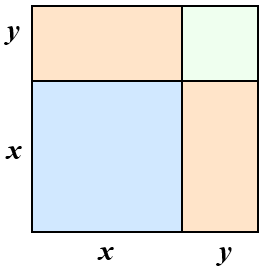
Solução
(a) Observe que podemos decompor a área [tex]x^2[/tex] do quadrado externo como soma das áreas [tex]A_1[/tex] , [tex]A_2[/tex] e [tex]A_3[/tex] mostradas na figura abaixo.
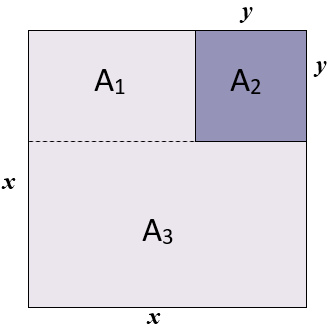
Assim, segue que:
[tex]\qquad x^2=A_1+A_2+A_3[/tex]
[tex]\qquad x^2=\left(x-y\right)\cdot y+y^2+\left(x-y\right)\cdot x[/tex]
[tex]\qquad x^2-y^2=\left(x-y\right)\cdot y+\left(x-y\right)\cdot x[/tex]
[tex]\qquad x^2-y^2=\left(x-y\right)\cdot x+\left(x-y\right)\cdot y[/tex]
[tex]\qquad x^2-y^2=\left(x-y\right)\cdot \left(x+y\right)[/tex]
Dessa forma, a figura exibida no item (a) mostra geometricamente o produto notável “diferença de quadrados“:
- [tex]\fcolorbox{black}{#eee0e5}{$ x^2-y^2=\left(x-y\right)\cdot \left(x+y\right)$}[/tex] .
(b) Para este item, vamos decompor a área [tex]\left(x+y\right)^2[/tex] do quadrado externo como soma das áreas [tex]A_1[/tex] , [tex]A_2[/tex] , [tex]A_3[/tex] e [tex]A_4[/tex] mostradas na figura abaixo.
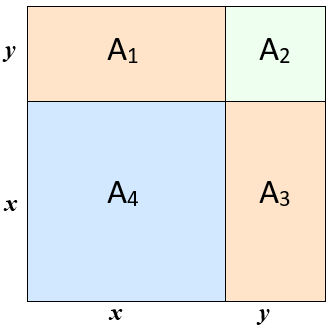
Assim, temos que:
[tex]\qquad \left(x+y\right)^2=A_1+A_2+A_3+A_4[/tex]
[tex]\qquad \left(x+y\right)^2=x\cdot y+y^2+x\cdot y+x^2[/tex]
[tex]\qquad \left(x+y\right)^2=2x\cdot y+y^2+x^2[/tex]
[tex]\qquad \left(x+y\right)^2=x^2+2x\cdot y+y^2[/tex]
Dessa forma, a figura exibida no item (b) mostra geometricamente o produto notável “quadrado da soma“:
- [tex]\fcolorbox{black}{#eee0e5}{$ \left(x+y\right)^2=x^2+2x\cdot y+y^2 $}[/tex] .
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
