Problema
(Indicado a partir do 8º ano do E. F.)
No triângulo [tex]ABC[/tex] os ângulos [tex]\widehat{A}[/tex] e [tex]\widehat B[/tex] medem [tex]60^\circ[/tex] e [tex]70^\circ[/tex], respectivamente. Os segmentos [tex]BD[/tex] e [tex]CE[/tex] são alturas do triângulo. Quanto mede o ângulo [tex]A\widehat E D[/tex]?
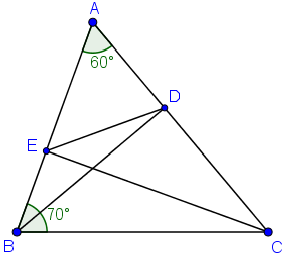

Lembretes
(1) A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex].
(2) As três alturas de um triângulo cortam-se num mesmo ponto (o ortocentro do triângulo).
(3) Se a soma dos ângulos opostos de um quadrilátero é [tex]180^\circ[/tex], então este quadrilátero é inscritível numa circunferência.
(4) Se dois ângulos inscritos enxergam o mesmo arco de circunferência, então eles são congruentes. (Para aprender mais sobre ângulos centrais e inscritos, dê uma passadinha por esta Sala de Estudos: Brincando com Geometria: Ângulo Central e Ângulo Inscrito.).
Solução
Leia com atenção as explicações de como obter as medidas que aparecem na figura abaixo.
- Pelo lembrete 1, temos que a medida do ângulo [tex]\hat{C}[/tex] pode ser assim calculada: [tex]\boxed{180^\circ-\textcolor{green}{70^\circ}-\textcolor{green}{60^\circ}=\textcolor{blue}{50^\circ}}[/tex].
- Traçando a altura do triângulo relativa ao vértice [tex]A[/tex], obtemos um ponto [tex]F[/tex] sobre o lado [tex]\overline{BC}[/tex] tal que a medida do ângulo [tex]A\hat{F}C[/tex] é [tex]90^\circ[/tex]. Portanto, novamente pelo lembrete 1, temos que a medida do ângulo [tex]C\hat{A}F[/tex] é [tex]\boxed{180^\circ-\textcolor{blue}{90^\circ}-\textcolor{blue}{50^\circ}=\textcolor{red}{40^\circ}}[/tex].
- Agora, chamando o ortocentro do triângulo de ponto [tex]O[/tex] (lembrete 2), observe que o quadrilátero [tex]AEOD[/tex] é inscritível numa circunferência. Com efeito, pelo enunciado, os ângulos opostos [tex]O\hat{E}A[/tex] e [tex]O\hat{D}A[/tex] são retos, logo somam [tex]180^\circ[/tex]. Pelo lembrete 3, existe uma circunferência que circunscreve o quadrilátero [tex]AEOD[/tex].
Mas aonde isto nos leva?
– Note que, nessa circunferência, os ângulos inscritos [tex]O\hat{E}D[/tex] e [tex]O\hat{A}D[/tex] enxergam o mesmo arco [tex]\stackrel{\frown}{OD}[/tex]. Logo, pelo lembrete 4, são congruentes.
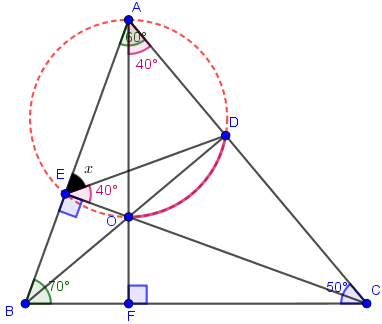
- Com isso, se [tex]x[/tex] é a medida em graus do ângulo [tex]A\hat E D[/tex], analisando os ângulos com vértices no ponto [tex]E[/tex] que formam o ângulo raso [tex]A\hat E B[/tex] , temos [tex]\boxed{x=180^\circ-\textcolor{red}{40^\circ}-\textcolor{blue}{90^\circ}=50^\circ}\, .[/tex]
Portanto, a medida do ângulo [tex]A\hat E D[/tex] é [tex] \fcolorbox{black}{#eee0e5}{$50^\circ$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
