Problema
(Indicado a partir do 9º ano do E. F.)
Segundo a Wikipédia, uma ponte estaiada (português brasileiro) ou ponte atirantada (português europeu) é um tipo de ponte suspensa por cabos constituída de um ou mais mastros, de onde partem cabos de sustentação para os tabuleiros da ponte.
Na cidade de Salto, SP, tem uma ponte estaiada sobre o rio Tietê.
 (Foto: Divulgação/Prefeitura de Salto)
(Foto: Divulgação/Prefeitura de Salto)
Segundo o site G1, essa ponte possui 225 metros de extensão, 15,5 metros de largura e um mastro com 40 metros de altura.
Suponhamos que uma das extremidades do maior cabo de sustentação esteja a uma altura de 35 metros e que a outra extremidade esteja a uma distância ao eixo central de 110 metros. Suponhamos também que uma das extremidades do menor cabo esteja a uma altura de 8 metros e que a outra extremidade esteja a uma distância ao eixo central de 20 metros. Considere ainda que todos os cabos de sustentação estejam igualmente espaçados, tanto na horizontal quanto na vertical.
Determine o comprimento dos dois menores e dos dois maiores cabos dentre os dez destacados em vermelho na figura abaixo.

Solução
Para resolvermos o problema basta fazer as continhas [tex]\boxed{\dfrac{35-8}{9}=3}[/tex] e [tex]\boxed{\dfrac{110-20}{9}=10}[/tex] e observarmos que, para cada lado da ponte, temos a seguinte configuração:
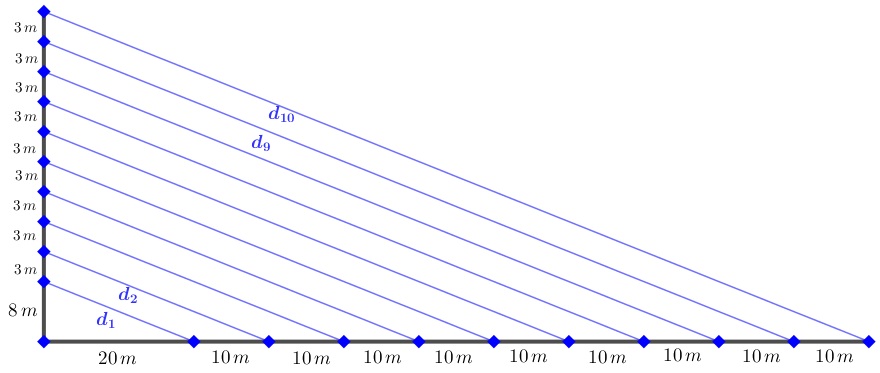
Para encontrarmos a solução, devemos calcular as distâncias [tex]d_1[/tex], [tex]d_2[/tex], [tex]d_9[/tex] e [tex]d_{10}[/tex] e para isso vamos utilizar o Teorema de Pitágoras:
- [tex] d_1^2=20^2+8^2=464 \\
\boxed{ d_1=4\sqrt{29} \, m} \, [/tex]; - [tex] d_2^2=30^2+11^2=1021 \\
\boxed{ d_2=\sqrt{1021} \, m} \, [/tex]; - [tex] d_9^2=100^2+32^2= 11024\\
\boxed{d_9=4\sqrt{689} \, m} \, [/tex]; - [tex] d_{10}^2=110^2+35^2= 13325 \\
\boxed{d_{10}=5\sqrt{533} \, m} \, [/tex].
Medidas aproximadas desses comprimentos seriam:
[tex]\qquad \fcolorbox{black}{#eee0e5}{$d_1\approx 21,54 \, m$} \, [/tex], [tex] \, \qquad\fcolorbox{black}{#eee0e5}{$d_2\approx 31,95 \, m$} \, [/tex], [tex] \, \qquad\fcolorbox{black}{#eee0e5}{$d_9\approx 105,00 \, m$} \, [/tex] e [tex] \, \qquad\fcolorbox{black}{#eee0e5}{$d_{10}\approx 115,43 \, m$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
