Problema
Um funcionário de um escritório, após um dia exaustivo de trabalho, escreveu na lousa da Sala de Reuniões a sequência dos números naturais de [tex]1[/tex] a [tex]100[/tex]. No dia seguinte, outro funcionário prolongou a sequência e registrou na mesma lousa os números naturais de [tex]101[/tex] a [tex]350[/tex].
A brincadeira continuou e, de repente, já estavam registrados ordenadamente na lousa todos os números naturais de [tex]1[/tex] a [tex]2018[/tex]. Então, alguém propôs apagar “matematicamente” os números registrados até aquele momento, substituindo dois números escritos na lousa pela média aritmética deles. Por exemplo, os números [tex]\boxed{1 \text{ e }3}[/tex] poderiam ser substituídos por uma segunda cópia do número [tex]\boxed{2}[/tex], já que [tex]\dfrac{1+3}{2}=2[/tex]; os números [tex]\boxed{2 \text{ e }5}[/tex] poderiam ser substituídos pelo número [tex]\boxed{3,5}[/tex], já que [tex]\dfrac{2+5}{2}=3,5.[/tex]
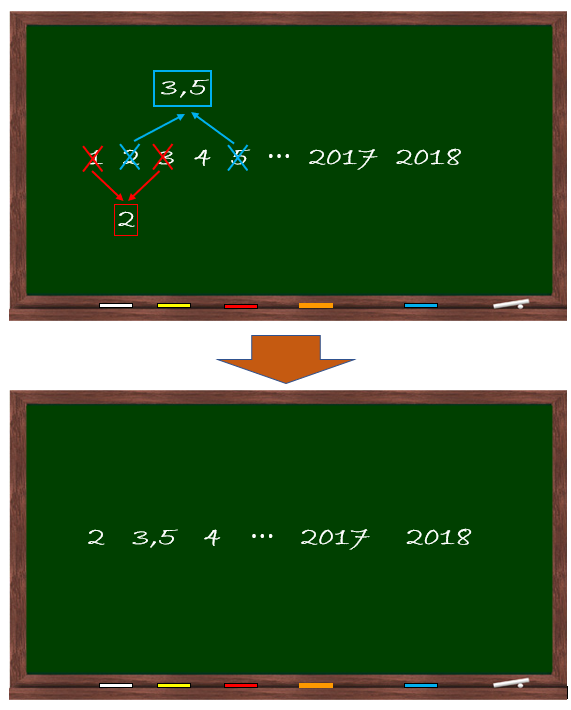
A partir da sequência inicial, é possível definir uma sequência de substituições desse tipo de modo que o último número restante na lousa seja o número [tex]\fcolorbox{black}{#C1FFC1}{$ 2 $}[/tex] ?
Solução
Sim, a partir da sequência inicial escrita na lousa do escritório podemos ficar apenas com um número [tex]2[/tex]. Observe.
- Primeiramente substitua os números [tex]2018[/tex] e [tex]2016[/tex] pela sua média aritmética, ou seja, [tex]2017[/tex], e a sequência
[tex]\qquad \fcolorbox{black}{#C1FFC1}{$1 \quad 2 \quad 3 \quad \cdots \quad 2015 \quad \textcolor{red}{2016} \quad 2017 \quad \textcolor{red}{2018}$}[/tex] - Ao fazermos a média dos dois números [tex]2017,[/tex] encontramos um único número [tex]2017[/tex] e a sequência
[tex]\qquad \fcolorbox{black}{#C1FFC1}{$1 \quad 2 \quad 3 \quad \cdots \quad 2015 \quad \textcolor{blue}{2017} \quad \textcolor{blue}{2017}$}[/tex]
torna-se
[tex]\qquad \fcolorbox{black}{#C1FFC1}{$1 \quad 2 \quad 3 \quad \cdots \quad 2015 \quad \textcolor{blue}{2017}$}.[/tex] - Podemos substituir os números [tex]2015[/tex] e [tex]2017[/tex] na sequência
[tex]\qquad \fcolorbox{black}{#C1FFC1}{$1 \quad 2 \quad 3 \quad \cdots \quad 2014 \quad \textcolor{#FF1493}{2015} \quad \textcolor{#FF1493}{2017}$}[/tex]
por [tex]2016[/tex], obtendo
[tex]\qquad \fcolorbox{black}{#C1FFC1}{$1 \quad 2 \quad 3 \quad \cdots \quad 2014 \quad \textcolor{#FF1493}{2016}$}.[/tex] - A seguir, substitua os números [tex]2014[/tex] e [tex]2016[/tex] por [tex]2015[/tex], obtendo
[tex]\qquad \fcolorbox{black}{#C1FFC1}{$1 \quad 2 \quad 3 \quad \cdots \quad 2013 \quad 2015 $}.[/tex]
fica
[tex]\qquad \fcolorbox{black}{#C1FFC1}{$1 \quad 2 \quad 3 \quad \cdots \quad 2015 \quad 2017 \quad \textcolor{red}{2017}$}.[/tex]
Procedendo de maneira análoga, após um número finito de passos, encontramos a sequência
[tex]\qquad \fcolorbox{black}{#C1FFC1}{$1 \quad 3$}[/tex]
e, substituindo os números [tex]1[/tex] e [tex]3[/tex] pela respectiva média, restará um único número na lousa:
[tex]\qquad \dfrac{1+3}{2}=\fcolorbox{black}{#C1FFC1}{$2$}.[/tex]
