Fórmulas de De Moivre
Dado um número complexo escrito na forma algébrica [tex]z=x+iy \, [/tex], podemos calcular a [tex]n[/tex]-ésima potência de [tex]z[/tex] pela definição, ou seja,
[tex]\qquad \qquad (x+iy)^n=\underbrace{(x+iy)(x+iy)\dots (x+iy)}_{n-vezes},[/tex]
e também a [tex]n[/tex]-ésima raiz [tex]z[/tex], ou seja, o número complexo [tex]w=u+iv[/tex], denotado por [tex]\sqrt[n]{z}[/tex], tal que
[tex]\qquad \qquad (u+iv)^n=x+yi=z[/tex].
Mas, quando [tex]n[/tex] for grande, essas operações podem ser muito trabalhosas!
Este problema pode ser contornado escrevendo o número complexo [tex]z[/tex] na forma trigonométrica. Vejamos como fazer isso.
Observe a figura abaixo e perceba que [tex]x=\rho \cos \theta[/tex] e [tex]y=\rho \, \mathrm{sen} \, \theta[/tex].
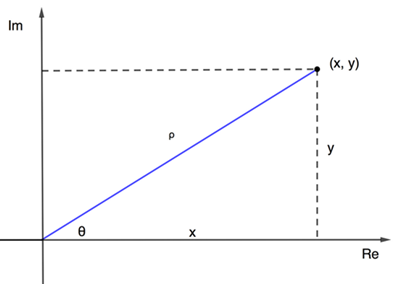
Assim, dado um número complexo escrito na forma algébrica [tex]z=x+iy[/tex], existe um número real positivo [tex]\rho=\sqrt{x^2+y^2}[/tex], conhecido como módulo de [tex]z[/tex], e um ângulo [tex]\theta[/tex], conhecido como argumento de [tex]z[/tex], tais que
[tex]\qquad \qquad x+iy=\rho(\cos \theta+i \, \mathrm{sen} \, \theta).[/tex]
Esta forma de se escrever números complexos é conhecida como forma trigonométrica.
Vejamos agora como multiplicar números complexos utilizando a forma trigonométrica, pois isso vai nos ajudar a obter mais facilmente a [tex]n[/tex]-ésima potência e a [tex]n[/tex]-ésima raiz de um dado número complexo [tex]z[/tex] ([tex]z^n[/tex] e [tex]\sqrt[n]{z}[/tex], respectivamente).
[tex]\qquad \qquad \begin{align*} z_1 z_2&=\rho_1 \rho_2(\cos \theta_1+i \, \mathrm{sen} \, \theta_1)(\cos \theta_2+i \, \mathrm{sen} \, \theta_2)\\
&=\rho_1 \rho_2[ \cos \theta_1 \cos \theta_2-\, \mathrm{sen} \, \theta_1 \, \mathrm{sen} \, \theta_2+i(\cos \theta_1 \, \mathrm{sen} \, \theta_2 +\cos \theta_2 \, \mathrm{sen} \, \theta_1)] \, .
\end{align*}[/tex]
(Lembre-se de que [tex]i^2=-1[/tex], por definição.)
Usando as fórmulas para o seno e o cosseno do arco soma obtemos, ainda:
[tex]\qquad \qquad z_1 z_2=\rho_1 \rho_2(\cos (\theta_1+\theta_2)+i(\, \mathrm{sen} \, (\theta_1+\theta_2))[/tex],
e podemos, então, observar que "multiplicar números complexos na forma trigonométrica equivale a multiplicar seus módulos e adicionar os seus argumentos". E isso continua válido para a multiplicação de mais de dois números complexos.
[tex] \textcolor{#800000}{(i)}[/tex] Assim, observe que se [tex]\boxed{z=\rho(\cos \theta+i \, \mathrm{sen} \, \theta)}[/tex], podemos concluir que [tex] \, \fcolorbox{black}{#eee0e5}{$z^n=\rho^n(\cos n\theta+i \, \mathrm{sen} \, n\theta)$} \, .[/tex]
Esta fórmula é conhecida como fórmula de potenciação de De Moivre ou primeira fórmula de De Moivre.
[tex] \textcolor{#800000}{(ii)}[/tex] Por outro lado, uma [tex]n[/tex]-ésima raiz de um número complexo [tex]z=\rho(\cos \theta+i \, \mathrm{sen} \, \theta)[/tex], deve ser um número complexo
[tex]\qquad w=\rho_w(\cos \theta_w+i \, \mathrm{sen} \, \theta_w)[/tex]
tal que
[tex]\qquad w^n=z=\rho (\cos \theta+i \, \mathrm{sen} \, \theta)[/tex].
Mas
[tex]\qquad w^n=\rho_w^n (\cos n\theta_w+i \, \mathrm{sen} \, n\theta_w)[/tex];
assim,
[tex]\qquad \rho_w^n=\rho \, [/tex] e [tex] \, n\theta_w=\theta[/tex].
É fácil ver que [tex]\rho_w=\sqrt[n]{\rho} \, [/tex] e que qualquer uma das [tex]n[/tex] escolhas [tex]\frac{\theta}{n}, \frac{\theta+2\pi}{n}\dots,\frac{\theta+(n-1)2\pi}{n}[/tex] para [tex]\theta_w[/tex] verifica [tex]n\theta_w=\theta[/tex].
Portanto, um número complexo [tex]\boxed{z=\rho(\cos \theta+i \, \mathrm{sen} \, \theta)}[/tex] possui muitas raízes [tex]n[/tex]-ésimas, mais especificamente, possui [tex]n[/tex] raízes [tex]n[/tex]-ésimas, cada uma dada por
[tex]\qquad \qquad \fcolorbox{black}{#eee0e5}{$\sqrt[n]{z}=\sqrt[n]{\rho}\left(\cos (\frac{\theta+2k\pi}{n})+i \, \mathrm{sen} \, (\frac{\theta+2k\pi}{n}) \right)$} \, , \qquad k=0, \dots, n-1.[/tex]
Esta fórmula é conhecida como fórmula de radiciação de De Moivre ou segunda fórmula de De Moivre.
