|
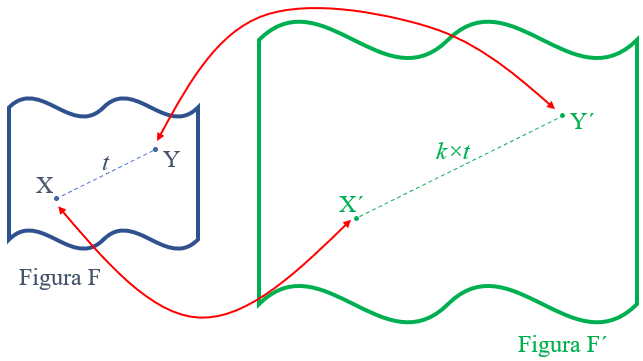
Ampliação e redução de figuras é um assunto presente no cotidiano das pessoas e muito importante no estudo da Geometria, pois envolve a questão da semelhança de figuras. No entanto, esse assunto gera, muitas vezes, dúvidas para aqueles que se deparam com situações teoricamente bem simples, como no problema apresentado a seguir. |
Problema
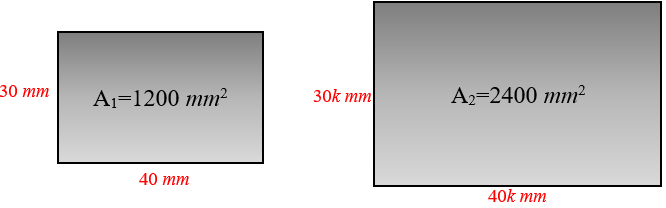
A imagem abaixo tem dimensões [tex]30\ mm \times 40\ mm.[/tex]

A partir dessa imagem, queremos fazer duas outras:
- uma com ampliação de [tex]100 \%[/tex];
- outra com redução de [tex]50 \%[/tex].
Quais serão as dimensões das novas imagens nas duas situações propostas?
|
Pois bem, mas o que o problema está realmente pedindo: |
 |
 |
Pois é… |
Inicialmente, duas perguntas:
O que é Ampliar?
O que é Reduzir?
– Segundo o site www.dicio.com.br, ampliação é o ato ou efeito de ampliar, é a reprodução de uma fotografia em tamanho maior, enquanto reduzir é tornar menor uma fotografia.
Mas será que essas definições ajudam
a resolver o problema proposto?
A princípio não, pois ainda não está claro o que devemos fazer para modificar a figura original a fim de obtermos os resultados pedidos.
Temos, de fato, duas interpretações que podem ser consideradas; a saber:
[tex]\qquad 1ª)[/tex] Ampliar ou reduzir as dimensões da figura original;
[tex]\qquad 2ª)[/tex] Ampliar ou reduzir o valor da área mantendo, claro, a proporcionalidade das suas dimensões.
Bem, uma coisa está firmada nessa discussão:
para não deformarmos a imagem do beija-flor.
Vamos ver, então, o que são figuras semelhantes.
A expressão " figuras semelhantes " é comumente utilizada para classificar figuras que se assemelham, figuras parecidas, figuras de mesma aparência. Mas, matematicamente falando, a definição geral de figuras semelhantes é um pouco complicada…
Para a discussão do problema, não precisaremos trabalhar com essa definição geral, pois queremos ampliar e reduzir um retângulo, que é um caso particular de polígono. Vamos então apresentar, inicialmente, a definição de polígonos semelhantes.
Polígonos semelhantes
Dois polígonos são semelhantes se satisfizerem simultaneamente as seguintes condições:
- os ângulos internos correspondentes são congruentes, isto é, têm medidas iguais;
- as medidas dos lados que se correspondem são proporcionais.
Quando dois polígonos são semelhantes, um é redução, ou é ampliação, ou uma cópia do outro.
Um caso importante desse tipo de semelhança é a "semelhança entre triângulos". Há uma Sala de Ajuda sobre triângulos semelhantes no nosso Blog! Dê uma passadinha por lá, mais tarde.
Por exemplo, observe as figuras abaixo.
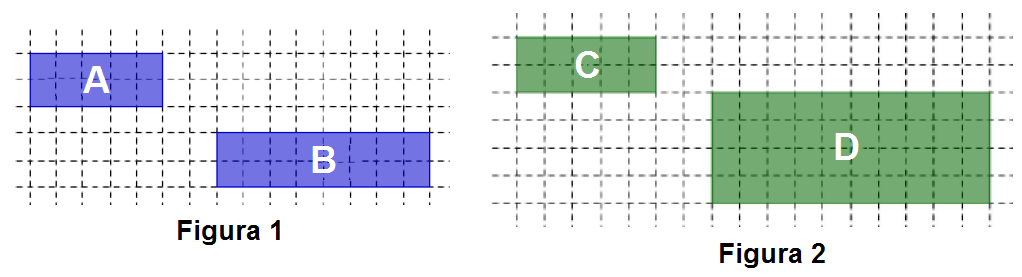
Tomemos por unidade de medida o lado de cada quadradinho da malha utilizada.
➤ Por outro lado, os retângulos C e D da Figura 2 são semelhantes, pois além de possuírem ângulos de mesma medida, a razão entre as medidas dos comprimentos dos segmentos que são bases, [tex]\dfrac{5}{10}=\dfrac{1}{2}[/tex], é igual à razão das medidas dos comprimentos dos segmentos que são alturas,[tex]\dfrac{2}{4}=\dfrac{1}{2}[/tex].
Observe, agora, as próximas figuras.

Considerando, mas uma vez, como unidade de medida o lado de cada quadradinho da malha, observe que:
➤ Por sua vez, os retângulos G e H são semelhantes, pois além de possuírem todos os ângulos retos, a razão entre as medidas dos comprimentos dos segmentos que são bases é igual à razão das medidas dos comprimentos dos segmentos que são alturas:[tex]\dfrac{4}{2}=2=\dfrac{6}{3}[/tex].
➤ Consequentemente, os quadriláteros F e H não são semelhantes.
 |
Fácil de entender? |
|
Até agora, tudo bem! |
 |
 |
Observe que, matematicamente falando, quando dois polígonos são semelhantes, um é redução, ou ampliação, ou cópia do outro. |
Vamos apresentar a definição geral de figuras semelhantes só por curiosidade; ela não será necessária no restante da discussão.
Para ver a definição, clique no botão a seguir.
|
Tá, entendi o que são polígonos semelhantes e quase entendi a definição geral. (Vou tentar entendê-la mais tarde.) Mas ainda não consigo saber se, para resolver o problema proposto, eu amplio/reduzo diretamente as dimensões ou amplio/reduzo diretamente as áreas… |
 |
 |
Da maneira com que o problema foi proposto, não dá para saber mesmo: as duas interpretações que você fez estão corretas! |
|
O jeito, então, é resolver das duas maneiras… |

|
 |
Perfeito, vamos fazer isso! |
- Primeiro caso: Ampliando as dimensões da imagem apresentada em [tex]100 \%[/tex]
Para ver a solução, clique no botão abaixo.
- Segundo caso: Ampliando a área da imagem apresentada em [tex]100 \%[/tex]
Para ver a solução, clique no botão abaixo.
- Terceiro caso: Reduzindo as dimensões da imagem apresentada em [tex]50 \%[/tex]
Para ver a solução, clique no botão abaixo.
- Quarto caso: Reduzindo a área da imagem apresentada em [tex]50 \%[/tex]
Para ver a solução, clique no botão abaixo.
|
As soluções propriamente ditas não são difíceis de se entender! |
|
 |
Ampliar [tex]x\%[/tex] e reduzir [tex]z\%[/tex] as dimensões, sem se preocupar diretamente com a área da figura original, talvez sejam as interpretações mais utilizadas no dia a dia das pessoas no que se refere às expressões "ampliar [tex]x\%[/tex] uma figura" e "reduzir [tex]z\%[/tex] uma figura". |
|
Em caso de dúvida, o que fazer? |
 |
 |
Se o problema foi proposto por uma pessoa que está por perto, questione-a sobre o tipo de ampliação desejado. Se o problema estiver em um livro, ou outro tipo de texto, peça ajuda ao seu professor ou à sua professora de matemática. |
|
E aprender a solucionar o problema, segundo as duas interpretações, também é uma boa pedida… |
|
Considerando os significados da palavra ampliar, que pode ser “tornar mais ampla a extensão ou a área de” ou “dar formato maior”, em algumas situações não precisamos de maiores especificações do que vai ser ampliado:
- Um colégio vai ampliar em 100% o número de vagas no próximo ano.
Aqui teríamos uma única interpretação, pois apenas uma única variável que pode ser ampliada aparece: o número de vagas. Neste caso, no próximo ano o colégio terá o dobro de vagas que tem neste ano. - A diretoria de um clube resolveu ampliar em 100% a área de lazer, que hoje é uma área retangular de 10 por 20 metros.
Neste caso, embora tenhamos dois números, o que vai ser ampliado corresponde ao produto deles: [tex]200[/tex]; e, se a forma da nova área for também retangular, não podemos dobrar as medidas, como no caso anterior, pois estaríamos quadruplicando a área.
Mas no caso da ampliação de uma fotografia temos duas interpretações:
- “ampliar 100% para ter uma área 100% maior”;
- “ampliar 100% para ter um perímetro 100% maior”, e talvez essa seja a interpretação mais utilizada no dia a dia das pessoas e nos problemas que aparecem nos livros de matemática.
Bem, na primeira interpretação teríamos mais de uma resposta: podemos aumentar em 100% a área da fotografia multiplicando os lados dela por raiz quadrada de 2 ou mantendo um dos lados com a mesma medida e dobrando a medida do segundo lado (aqui com uma possível deformação). Na segunda interpretação, se mantivermos a forma da fotografia, teríamos apenas uma resposta: dobrar os comprimentos dos lados.
Para se evitar ambiguidade, a formulação da pergunta do problema em questão poderia ser mais específica:
-
➤ […] A partir dessa imagem, queremos fazer duas outras:
- uma com ampliação de [tex]100 \%[/tex] “de sua área”;
- outra com redução de [tex]50 \%[/tex] “de sua área”.
Quais serão as dimensões das novas imagens nas duas situações propostas?
ou
- ➤ […] A partir dessa imagem, queremos fazer duas outras:
- uma com ampliação de [tex]100 \%[/tex] “do comprimento de seus lados”;
- outra com redução de [tex]50 \%[/tex] “do comprimento de seus lados”.
Quais serão as dimensões das novas imagens nas duas situações propostas?
Estabelecido o significado do ampliar ou do reduzir, a matemática estabelece o que fazer para se resolver o problema:
Ampliando ou reduzindo as dimensões de uma fotografia
➤ Ampliar [tex]k[/tex] vezes as dimensões de uma fotografia, [tex]k \gt 1[/tex], significa obtermos outra fotografia maior semelhante à primeira na qual suas dimensões são [tex]k[/tex] vezes as dimensões da fotografia original.
➤ Já reduzir uma fotografia [tex]k[/tex] vezes, [tex]0 \lt k \lt 1[/tex], significa obtermos outra fotografia menor semelhante à primeira cujas dimensões são [tex]k[/tex] vezes as dimensões da fotografia original.
Neste caso, embora não se tenha preocupação direta com a área da figura resultante, sabemos que a razão entre as medidas das áreas de duas figuras semelhantes é [tex]k^2.[/tex]
Observação: Em livros didáticos, o número [tex]k[/tex] é chamado de razão de semelhança (ou fator de ampliação/redução).
Ampliando ou reduzindo a área de uma fotografia
➤ Ampliar [tex]k[/tex] vezes a área de uma fotografia, [tex]k \gt 1[/tex], significa obtermos outra figura maior, semelhante à primeira, cuja medida da área seja [tex]k[/tex] vezes a medida da área da fotografia original.
➤ Reduzir [tex]k[/tex] vezes a área de uma fotografia, [tex]0 \lt k \lt 1[/tex], significa obtermos outra figura menor, semelhante à primeira, cuja medida da área seja [tex]k[/tex] vezes a medida da área da fotografia original.
Neste caso, cálculos serão feitos para se determinar um valor [tex]t[/tex] tal que, ao ampliar/reduzir as dimensões da fotografia original [tex]t[/tex] vezes, a fotografia obtida tenha uma área cuja medida seja [tex]k[/tex] vezes maior/menor que a da fotografia original. (Você saberia fazer esses cálculos e determinar o valor de [tex]t[/tex]? Que tal tentar?)
Leitura complementar
Texto [tex]1[/tex] – Ampliando e reduzindo figuras: ontem e hoje
Atualmente, com a infinidade de recursos tecnológicos, ampliar, reduzir, reproduzir, rotacionar, inverter e deformar imagens são operações fáceis, mesmo para aqueles sem talento para o desenho. Mas, antes desses avanços muitas dessas transformações eram feitas com sistemas articulados desenvolvidos para fins específicos.
Um exemplo desses sistemas é o pantógrafo (panto, que significa ‘tudo’; grafo: que significa ‘escrever’). O modelo simples é constituído por quatro réguas articuladas e fixadas entre si. Duas réguas estão por baixo e as restantes são colocadas sobre as outras duas. A origem do pantógrafo é incerta, mas há registros de que já era utilizado, por povos, há mais de 2000 anos. O pantógrafo já foi muito utilizado em diversas áreas: na Geografia, possibilitando confeccionar mapas; na Engenharia, facilitando na confecção de plantas de construções; na serralheria, servindo para cortar chapas metálicas; em ourivesaria, sendo empregado para fazer gravações em alianças, anéis, medalhas, etc.
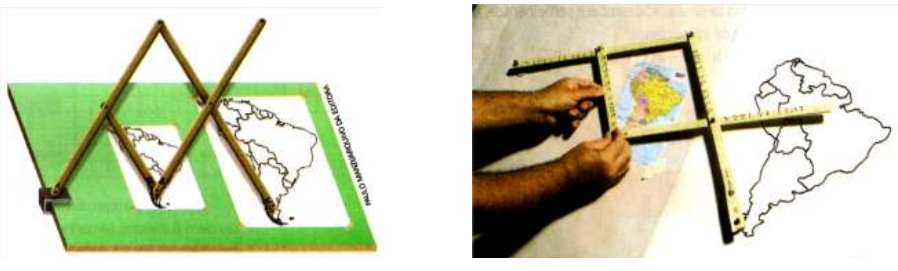
Extraído de Plano de aula: Ampliando e/ou reduzindo figuras planas
Pantógrafo – Ida Brandão
Extraído de https://freewareneesite.files.wordpress.com
Alguns vídeos interessantes
Ampliação ou redução?
Ampliador de desenhos (PANTÓGRAFO)
Figuras e polígonos semelhantes
Razão de semelhança vista como uma ampliação e redução
 |
Visite também a nossa Sala de Atividades Proporção em Geometria. |
Equipe COM – OBMEP
Setembro de 2020.
[1] Nova Escola – Plano de aula: Ampliando e/ou reduzindo figuras planas (Último acesso em 26/08/19)
[2] Ampliando os horizontes geométricos (Último acesso em 26/08/19)
[3] REde mATemaTICa – NOÇÃO DE SEMELHANÇA (Último acesso em 26/08/19)
[4] Fundação Cecierj – Semelhança de polígonos (Último acesso em 26/08/19)
[5] PANTÓGRAFO (Último acesso em 26/08/19)
[6] Matemática das Transformações-UFRGS (arquivo em pdf)