.Sala para leitura_007: Circunferências – Definições básicas
Muitas vezes não conseguimos entender ou aprender algo em matemática simplesmente porque não temos domínio da linguagem utilizada.
É como conversar com uma pessoa que fala japonês, sem conhecer esse idioma, não é?
Exatamente…
E como a compreensão da linguagem facilita o entendimento das ideias, vamos estabelecer algumas definições básicas para o estudo de circunferências, assunto que apareceu em várias discussões no nosso Blog.
Circunferência- Definições básicas
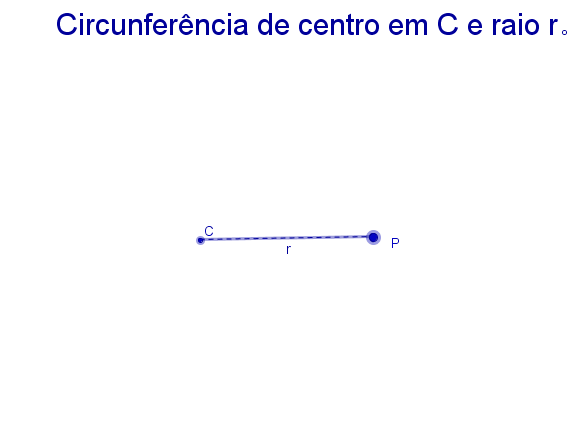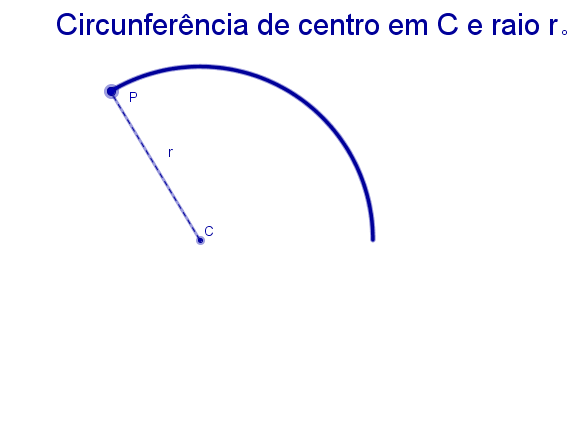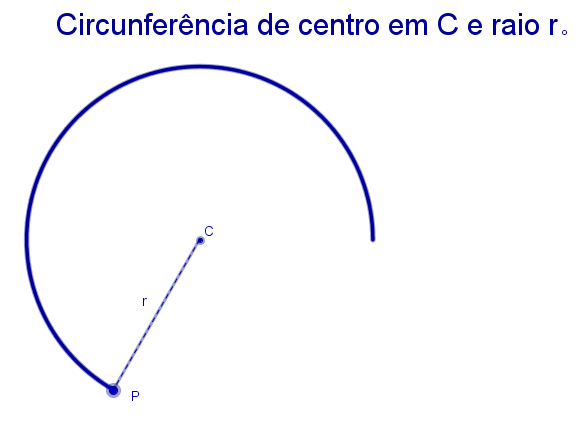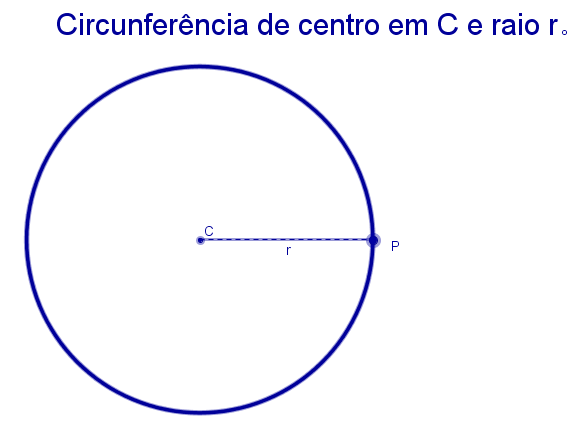
A definição inicial não poderia ser outra que não a de circunferência, não é?
Então, aí vai …
Clique no botão abaixo para ver a animação de uma circunferência de centro C e raio CP sendo traçada.
Leiam com atenção o que se segue. Apresentaremos outros elementos importantes de uma circunferência.
1) Abra o applet e aguarde o arquivo carregar.
2) Para reiniciar a construção, clique nas setinhas que aparecem no canto superior direito do applet .
OBMEP_ srdg, criado com o GeoGebra Observamos que a planilha ajuda na visualização do resultado; mas, matematicamente, não substitui sua demonstração.
Fixados um plano e uma circunferência desse plano, é interessante observarmos que podemos relacionar cada ponto do plano com a circunferência.
Vale a pena recordarmos que relação é essa.
Com o applet abaixo é possível várias cordas de uma circunferência fixada c.
Clique no botão e siga as instruções.
1) Abra o applet, aguarde o arquivo carregar e leia as instruções nele contidas.
2) Clique nos quadradinhos correspondentes às suas opções.
3) Para reiniciar a construção, clique nas setinhas que aparecem no canto superior direito do applet .
OBMEP_ srdg, criado com o GeoGebra Observamos que a planilha ajuda na visualização do resultado; mas, matematicamente, não substitui sua demonstração.
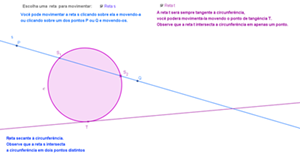
Ao observarmos as possíveis posições relativas entre uma circunferência e uma reta, encontramos duas posições que são bastante exploradas em problemas envolvendo circunferências.
Vale a pena registrá-las aqui!
Com o applet abaixo é possível movimentar duas retas, r e s, de modo a verificar
se as mesmas são secantes ou tangentes à uma circunferência fixada c.
É só clicar no botão e seguir as instruções.
Clique sobre a figura, o applet irá abrir em outra janela.
Equipe COM – OBMEP
Setembro de 2017.
Se for conveniente, copie os arquivos abaixo e utilize-os off-line em seu computador.
Mas não se esqueça de visitar este site e fazer a instalação da versão do GeoGebra adequada ao dispositivo.
