Problema
(A partir da 1ª série do E. M.- Nível de dificuldade: Fácil)
O gráfico de uma função [tex]f[/tex] é definido por três segmentos de reta e está representado na figura a seguir.
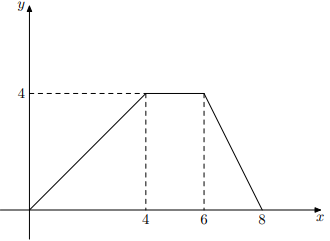
(a) Determine [tex]f(1)+f(2) +f(3)+ f(4)+f(5)+f(6)+f(7)+f(8)\,.[/tex]
(b) Você conhece a notação de somatório? Em caso positivo, indique a soma que você fez, utilizando tal notação.
Adaptado do PROFMAT – Exame Nacional de Acesso, 2017.
Solução
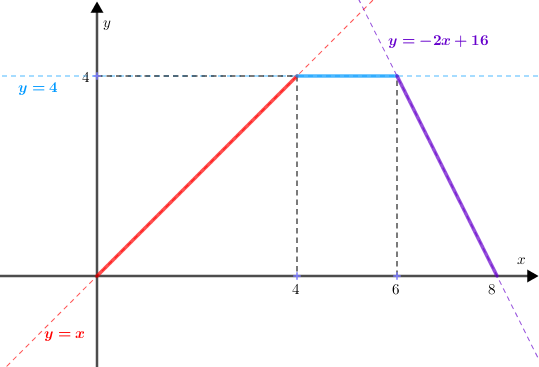
Na figura a seguir, destacamos com cores distintas os segmentos que definem o gráfico da função [tex]f[/tex] e traçamos as retas suporte de cada um deles.
Observe que:
- A reta suporte do segmento vermelho passa pelos pontos [tex]\left(0,0\right)[/tex] e [tex]\left(4,4\right)[/tex]; assim, sua equação com relação ao plano cartesiano [tex]xOy\,[/tex] é [tex]\, \textcolor{red}{y=x}\,.[/tex]
- A reta suporte do segmento azul é a reta horizontal que passa pelo ponto [tex]\left(4,4\right)[/tex]; assim, sua equação com relação ao plano cartesiano [tex]xOy\,[/tex] é [tex]\, \textcolor{#0099FF}{y=4}\,.[/tex]
- Para obter a equação da reta suporte do segmento roxo teremos que fazer algumas continhas.
A reta não é vertical; logo, ela tem equação reduzida, digamos, [tex]\textcolor{#6600CC}{y=ax+b}[/tex]. Como ela passa pelos pontos [tex]\left(8,0\right)[/tex] e [tex]\left(6,4\right)[/tex], temos o seguinte sistema de equações:
[tex]\qquad \begin{cases}0=8a+b\\
4=6a+b \end{cases}\;.[/tex]
Fazendo a diferença das duas equações, obtemos que [tex]2a=-4[/tex], donde segue que [tex]a=-2[/tex]. Substituindo esse valor na primeira equação do sistema, obtemos [tex]b=16\,.[/tex] Portanto, a equação da reta suporte do segmento roxo é [tex]\, \textcolor{#6600CC}{y=-2x+16}\,.[/tex]
(a) Pronto, já conseguimos determinar as imagens que compõem a soma definida no problema:
[tex]\quad f(1)=1\,;\,f(2)=2\,;\, f(3)=3\,;\,f(4)=4\,;\,f(5)=4\,;\,f(6)=4\,;\,f(7)=2\,;\,f(8)=0\,.[/tex]
Portanto,
[tex]\quad \fcolorbox{black}{#eee0e5}{$f(1)+f(2) +f(3)+ f(4)+f(5)+f(6)+f(7)+f(8)=$}[/tex]
[tex]\quad\quad \fcolorbox{black}{#eee0e5}{$=1+2+3+4+4+4+2+0=20$}\,.[/tex]
(b) Usando a notação de somatório, podemos reescrever a soma que fizemos como [tex]\,\fcolorbox{black}{#eee0e5}{$\sum\limits_{n=1}^{8}f(n)=20$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
