Problema
(A partir da 1ª série do E. M.- Nível de dificuldade: Difícil)
Determine a solução do sistema de inequações abaixo.
[tex]\qquad \qquad \begin{cases}
x^4-13x^2+36 \lt 0\\
\,\\
\dfrac{3x-12}{x+2}\leqslant 1
\end{cases}\;[/tex]

Lembretes
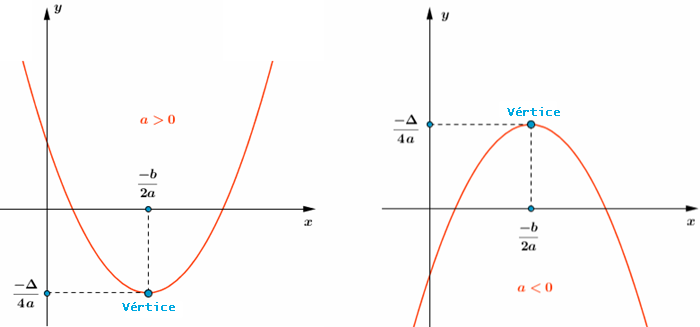
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,\, a\not=0[/tex], é uma parábola com eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola são dadas por [tex](x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex], sendo que [tex]x_v=\dfrac{-b}{2a}\, [/tex] e [tex]\, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
Solução
Para determinar a solução do sistema de inequações dado, vamos determinar a solução de cada desigualdade e fazer a interseção das duas soluções.
- (I) Observe, inicialmente, a seguinte sequência de desigualdades equivalentes:
- Em um plano cartesiano [tex]xOy[/tex] as equações [tex]y=x+2\,[/tex] e [tex]\,y=2x-14[/tex] definem duas retas oblíquas, a primeira cortando o eixo [tex]Ox[/tex] em [tex]x=-2[/tex] e a segunda em [tex]x=7.[/tex]
Veja um esboço do gráfico das duas retas: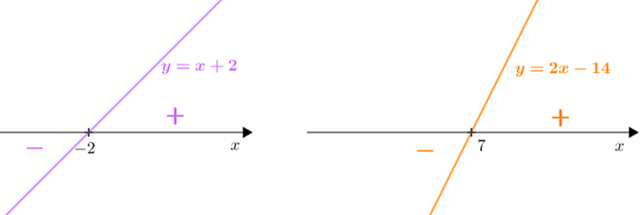
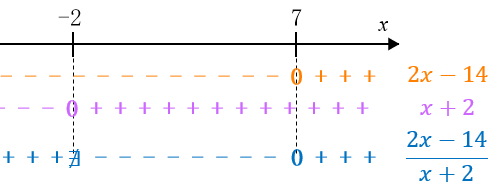
e o estudo da variação de sinal do quociente [tex]\dfrac{2x-14}{x+2}[/tex]:
- Analisaremos o sinal da função [tex]f:\mathbb{R}\rightarrow \mathbb{R}[/tex] definida por [tex]f(t)=t^2-13t+36[/tex]. Lembramos que analisar o sinal de uma função significa determinar quais valores do seu domínio têm imagens iguais a zero, quais têm imagens positivas e quais têm imagens negativas. No nosso caso, queremos determinar os valores de [tex]t[/tex] que têm imagens negativas.
Em um plano cartesiano [tex]tOy[/tex] o gráfico de [tex]f[/tex] define uma parábola com eixo de simetria paralelo ao eixo [tex]Oy[/tex] e concavidade voltada para cima. Para traçar um esboço dessa parábola e analisar a variação de sinal de [tex]f[/tex], vamos precisar das raízes da equação de segundo grau [tex]t^2-13t+36=0[/tex]. São elas: - Os gráficos das funções [tex]g,h:\mathbb{R}\rightarrow \mathbb{R}[/tex] em um plano cartesiano [tex]xOy[/tex] são parábolas com seus respectivos eixos de simetria paralelos ao eixo [tex]Oy[/tex] e concavidades voltadas para cima.
[tex]\qquad \begin{align*}\boxed{\dfrac{3x-12}{x+2}\leqslant 1} &\iff \dfrac{3x-12}{x+2}-1\leqslant 0\iff\\
& \iff \dfrac{(3x-12)-(x+2)}{x+2}\leqslant 0 \iff\\
& \iff\dfrac{3x-12-x-2}{x+2}\leqslant 0 \iff \\
&\iff \boxed{\dfrac{2x-14}{x+2}\leqslant 0}\,. \end{align*} [/tex]
Assim, podemos determinar a solução da inequação [tex]\boxed{\dfrac{3x-12}{x+2}\leqslant 1} [/tex] fazendo o estudo de variação de sinal da expressão [tex]\boxed{\dfrac{2x-14}{x+2}} [/tex] e determinando para quais valores reais de [tex]x[/tex] essa expressão é não positiva (negativa ou zero). Para isso, vamos estudar a variação de sinal do numerador e do denominador da fração.
O estudo da variação de sinal do quociente poderia também ser feito observando que:
[tex]\qquad \begin{cases} 2x-14 \gt 0 \iff 2x \gt 14 \iff x \gt 7; \\
2x-14 = 0 \iff 2x = 14 \iff x = 7; \\
2x-14 \lt 0 \iff 2x \lt 14 \iff x \lt 7. \end{cases}[/tex]
e
[tex]\qquad \begin{cases} x+2 \gt 0 \iff x \gt -2; \\
x+2 = 0 \iff x = -2; \\
x+2 \lt 0 \iff x \lt -2. \end{cases}[/tex]
De toda forma,
[tex]\qquad \textcolor{#0c66ff}{\dfrac{2x-14}{x+2}\leqslant 0 \iff -2 \lt x \leqslant 7}[/tex]
e, portanto, a solução da inequação [tex]\dfrac{3x-12}{x+2}\leqslant 1 [/tex] é o intervalo [tex]\fcolorbox{black}{#b8cae9}{$S_1=]-2,7]$}\,.[/tex]
(II) Para determinarmos a solução da desigualdade [tex]x^4-13x^2+36 \lt 0[/tex] teremos um pouquinho mais de trabalho!
Inicialmente, faremos uma mudança de variável: [tex]x^2=t[/tex]. Com isso, a desigualdade [tex]x^4-13x^2+36 \lt 0[/tex] passará a ser escrita como [tex]t^2-13t+36 \lt 0[/tex] e faremos, então, o estudo de variação de sinal da expressão [tex]t^2-13t+36[/tex] para determinarmos quais os valores reais de [tex]t[/tex] que tornam essa expressão negativa. Vamos lá!
[tex]\qquad t=\dfrac{-(-13)\pm\sqrt{(-13)^2-4\cdot 1\cdot 36 }}{2 \cdot 1}\\
\qquad t=\dfrac{13\pm\sqrt{169-144}}{2}\\
\qquad t=\dfrac{13\pm\sqrt{25}}{2} \\
\qquad t_1=\dfrac{13-5}{2}=4 \qquad \text{e}\qquad t_2=\dfrac{13+5}{2}=9\,. [/tex]
Veja um esboço do gráfico de [tex]f[/tex]:
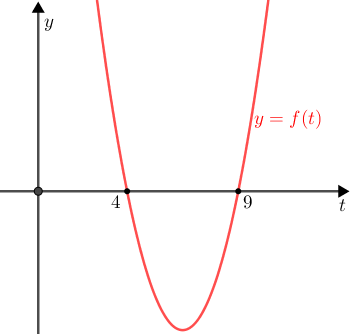
e sua variação de sinal:

Logo, [tex]\textcolor{red}{t^2-13t+36 \lt 0 \iff 4 \lt t \lt 9}[/tex].
Voltando à variável inicial [tex]x[/tex], temos que [tex]x^4-13x^2+36 \lt 0 \iff 4 \lt x^2 \lt 9[/tex]. Com isso, precisamos determinar para quais valores reais de [tex]x[/tex] temos [tex]4 \lt x^2 \lt 9[/tex].
Observe que [tex]4 \lt x^2 \lt 9[/tex] é equivalente a duas desigualdades simultâneas: [tex]4 \lt x^2\,[/tex] e [tex]\, x^2 \lt 9[/tex]. Assim, para obter a solução da segunda desigualdade que compõe o sistema inicial definido no problema, vamos resolver essas duas novas inequações e fazer a interseção de suas soluções.
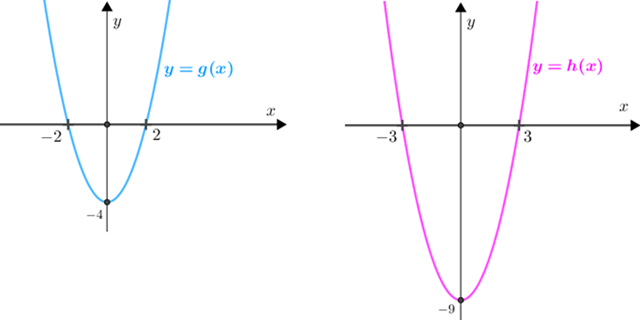
Para isso, vamos fazer o estudo da variação de sinal das funções [tex]g,h:\mathbb{R}\rightarrow \mathbb{R}[/tex] definidas por [tex]g(x)=x^2-4\,[/tex] e [tex]\, h(x)=x^2-9[/tex], uma vez que [tex]\boxed{4 \lt x^2 \iff 0 \lt x^2-4}\,[/tex] e [tex]\, \boxed{x^2 \lt 9 \iff x^2-9 \lt 0}\,.[/tex]
Para um esboço dessas parábolas vamos determinar as raízes das equações do segundo grau [tex] x^2-4=0\,[/tex] e [tex]\, x^2-9=0[/tex]:
[tex]\begin{array}{l|l}
\quad \quad x^2-4=0 \quad & \quad x^2-9=0\\
\quad \quad x^2=4 \quad & \quad x^2 =9\\
\quad \quad x_1=2 \qquad \text{e}\qquad x_2=-2\,. \quad & \quad x_3=3 \qquad \text{e}\qquad x_4=-3\,.\\
\end{array}[/tex]
A partir dessas raízes, obtemos um esboço dos gráficos de [tex]g\,[/tex] e [tex]\,h\,:[/tex]
e as duas variações de sinais de que precisamos:
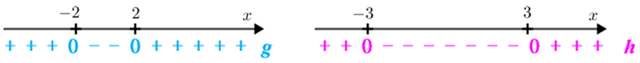
A pergunta cuja resposta fornecerá a solução [tex]S_2[/tex] da desigualdade [tex]x^4-13x^2+36 \lt 0[/tex] é: para que valores reais de [tex]x[/tex] temos [tex]\boxed{0 \lt x^2-4}\,[/tex] e [tex]\, \boxed{x^2-9 \lt 0}[/tex] ?
Vamos olhar as duas últimas variações de sinal juntas para responder a essa pergunta e determinarmos [tex]S_2[/tex]:
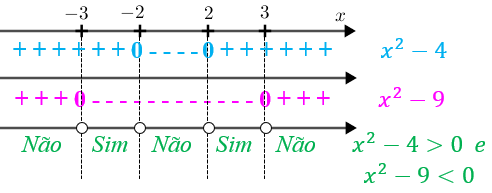
portanto, [tex]\fcolorbox{black}{#d2ffe6}{$S_2=]-3,-2[ \cup ]2,3[$}[/tex].
Finalmente, por (I) e por (II), a solução [tex]S[/tex] do sistema de inequações proposto no problema já pode ser calculada:
[tex]\qquad S=\textcolor{#0c66ff}{S_1} \cap\textcolor{#00B050}{S_2}[/tex]
[tex]\qquad S=\textcolor{#0c66ff}{]-2,7]} \cap \left(\textcolor{#00B050}{]-3,-2[ \cup ]2,3[}\right)[/tex]
[tex]\qquad S=]2,3[\,.[/tex]

Portanto, a solução do sistema de desigualdades proposto é [tex]\, \fcolorbox{black}{#eee0e5}{$S=]2,3[=\{x \in \mathbb{R} \text{ tais que } 2 \lt x \lt 3\}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |