✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
Seja [tex] \, q \, [/tex] um número real positivo.
Dentre todos os retângulos de perímetro [tex]2q[/tex], determine aquele que tem área máxima!

Lembretes
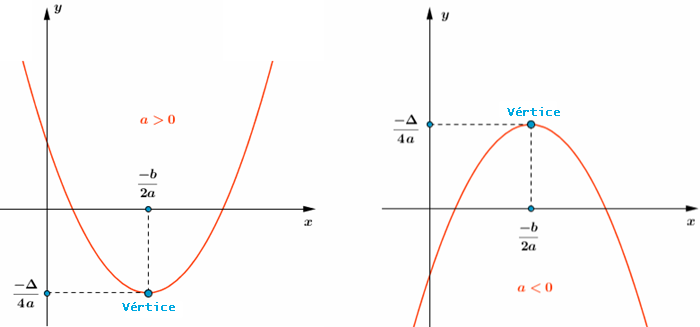
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c, \, a\not=0[/tex], é uma parábola com diretriz paralela ao eixo [tex]Ox[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola são dadas por [tex](x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex], sendo que [tex]x_v=\dfrac{-b}{2a} \, [/tex] e [tex] \, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
Solução
Vamos considerar um retângulo genérico cujos lados tenham comprimentos [tex]x \, [/tex] e [tex] \, y[/tex].
Assim, a área [tex] \, A \, [/tex] e o perímetro [tex] \, P \, [/tex] desse retângulo serão dados por:
- [tex]A=xy[/tex]
- [tex]P=x+y+x+y=2x+2y=2\left(x+y\right).[/tex]
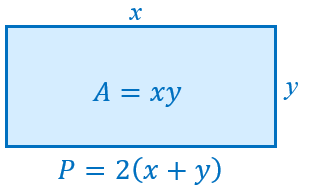
Neste problema, vamos considerar todos os retângulos cujos perímetros sejam [tex]2q[/tex], com [tex] \, q \, [/tex] um número real positivo fixo. Assim, teremos que:
[tex]\qquad P=2\left(x+y\right)[/tex]
[tex]\qquad \cancel{2}q=\cancel{2}\left(x+y\right)[/tex]
[tex]\qquad q=x+y[/tex]
[tex]\qquad y=q-x.[/tex]
Observe que o comprimento [tex] \, y \, [/tex] é função de [tex] \, x \, [/tex], já que [tex] \, q \, [/tex] é constante. Dessa forma, como [tex]A=xy[/tex], segue que:
[tex]\qquad A=x\left(q-x\right)[/tex]
[tex]\qquad A=qx-x^2[/tex]
e [tex]A[/tex] é também função de [tex]x.[/tex]
Vamos interpretar geometricamente os cálculos algébricos que fizemos até aqui:
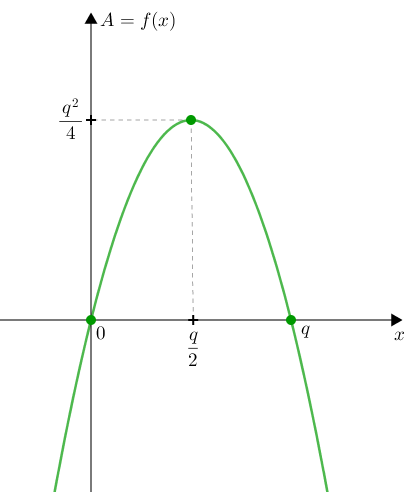
- Temos uma família de retângulos cujas respectivas áreas podem ser escritas em função do comprimento [tex]x[/tex] de um de seus lados como [tex]A=qx-x^2 \, [/tex], sendo [tex] \, q \, [/tex] um número real positivo fixo, ou seja, uma constante positiva.
Assim, voltando à Álgebra, fixado um número [tex]q \, [/tex], [tex]q \gt 0 \, [/tex], a cada retângulo cujos lados têm comprimentos [tex]x[/tex] e [tex]q-x[/tex] associamos de maneira única um número [tex]A[/tex] dado por [tex]A=qx-x^2[/tex]. Temos então uma função [tex]f[/tex] assim definida:
[tex]\qquad \begin{align*} f: \, \mathbb{R} \, &\rightarrow \, \mathbb{R}\\
x \, &\mapsto \, -x^2+qx
\end{align*}[/tex]
A geometria do nosso problema indica que, dentre todos os retângulos de perímetro [tex]2q[/tex], determinemos aquele que tem área máxima. De acordo com os nossos Lembretes, o gráfico da nossa função [tex]f[/tex] é uma parábola com a concavidade voltada para baixo; assim, vamos determinar o valor máximo que essa função [tex]f[/tex] assume. Ainda segundo nossos Lembretes, a primeira e a segunda coordenadas do vértice da parábola são, respectivamente, o ponto de máximo e o valor máximo da função [tex]f[/tex]:
[tex]\qquad x_v=\dfrac{-b}{2a}=\dfrac{-q}{-2}=\dfrac{q}{2}.[/tex]
[tex]\qquad A_v=\dfrac{-\Delta}{4a}=-\dfrac{\left(q^2-0\right)}{-4}=\dfrac{q^2}{4}[/tex]
Assim, a área máxima é [tex]\dfrac{q^2}{4}[/tex] e essa área é relativa ao retângulo cujo comprimento [tex]x[/tex] do lado é [tex]x=\dfrac{q}{2}[/tex].
Como o segundo comprimento do retângulo é [tex]y=q-x \, [/tex], segue que [tex]y=q-\dfrac{q}{2}=\dfrac{q}{2}.[/tex]
Portanto, fixadas as unidades de comprimento e de área, dentre todos os retângulos de perímetro [tex]2q[/tex], aquele que tem área máxima é o quadrado de lados com comprimento [tex]\dfrac{q}{2}[/tex] e essa área máxima é [tex]\dfrac{q^2}{4}.[/tex]
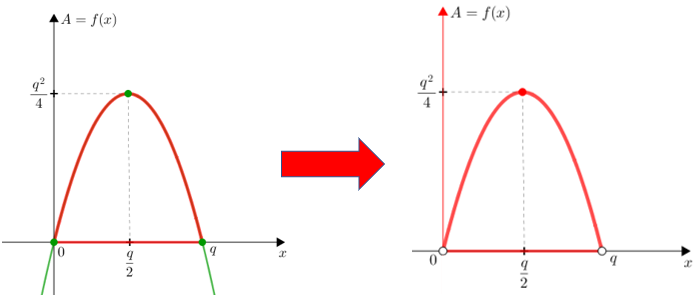
Analisando mais detalhadamente a geometria do problema, observamos que nem necessitaríamos da função [tex]f[/tex] definida em todo o seu domínio e o seu contradomínio.
Perceba que [tex]\boxed{x}[/tex] é o comprimento de um dos lados de um suposto triângulo de perímetro [tex]2q[/tex] e a esse [tex]x[/tex] associamos o número real positivo [tex]\boxed{qx-x^2} \, [/tex], ou seja, temos que [tex]\boxed{x \in \mathbb{R}_+^*} \, [/tex] e [tex] \, \boxed{qx-x^2 \in \mathbb{R}_+^*} \, [/tex]. Mais do que isso, perceba também que, como [tex]x \gt 0[/tex], então [tex]x \lt 2x \lt P=q[/tex].
Dessa forma, temos de fato [tex]\boxed{0\lt x \lt q} \, [/tex] e [tex] \, \boxed{f(x)=qx-x^2 \in \mathbb{R}_+^*}[/tex] e podemos considerar a função [tex]f[/tex] restrita a esses valores. (Estamos indicando por [tex]\mathbb{R}_+^*[/tex] o conjunto dos números reais positivos, ou seja, o intervalo [tex]] 0 \, , \, +\infty [ \, .[/tex])
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |