✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 1º ano do E. M. – Nível de dificuldade: Médio)
(OME – Olimpiada Matemática Española, 2001) Os comprimentos dos lados de um triângulo retângulo estão em progressão geométrica.
Determinar a razão [tex]r[/tex] dessa progressão.
Lembrete
Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
Solução
- Observe, inicialmente, que a razão [tex]r[/tex] de uma progressão pode ser [tex]1[/tex], maior do que [tex]1[/tex] ou menor do que [tex]1[/tex]. Na nossa solução vamos supor [tex]r\gt 1[/tex], pois:
- se considerássemos [tex]r=1[/tex], as três medidas seriam iguais e isso não seria possível, visto que o Teorema de Pitágoras nos assegura que, em um triângulo retângulo, a hipotenusa é maior do que os dois catetos.
- se considerássemos [tex]0 \lt r \lt 1[/tex], obteríamos as mesmas medidas dos lados, só que em ordem inversa.
- Observe também que o lado com a menor medida é um dos dois catetos do triângulo; pois, em um triângulo retângulo, a hipotenusa é maior do que os dois catetos.
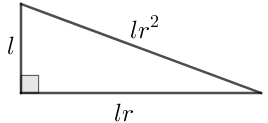Seja [tex]l[/tex] unidades de comprimento a medida do menor lado do triângulo retângulo em questão. Logo, as medidas dos outros lados serão [tex]l\,r\;[/tex] e [tex]\;l\,r^2[/tex] unidades de comprimento.
Pelo Teorema de Pitágoras, segue que:
[tex]\qquad l^2+\left(lr\right)^2=\left(lr^2\right)^2[/tex]
[tex]\qquad \cancel{l^2}+\cancel{l^2}\,r^2=\cancel{l^2}\,r^4[/tex]
[tex]\qquad 1+r^2=r^4[/tex]
[tex]\qquad r^4-r^2-1=0\,.\qquad \qquad \textcolor{#80000}{(i)}[/tex]
Precisamos, então, resolver a equação biquadrada [tex]\textcolor{#80000}{(i)}[/tex] e para isso vamos fazer uma mudança de variável: [tex]x=r^2\,.[/tex]
Observe:
[tex]\qquad r^4-r^2-1=0\ [/tex]
[tex]\qquad x^2-x-1=0 [/tex]
[tex] \qquad x=\dfrac{-(-1)\pm \sqrt{(-1)^2-4\cdot 1\cdot (-1)}}{2\cdot 1}[/tex]
[tex] \qquad x=\dfrac{1\pm \sqrt{1+4}}{2}=\dfrac{1\pm \sqrt{5}}{2}[/tex]
[tex] \qquad x_1=\dfrac{1+\sqrt{5}}{2}\quad[/tex] e [tex] \quad x_2=\dfrac{1-\sqrt{5}}{2}.[/tex]
Agora, precisamos obter o valor de [tex]r[/tex] e para tanto vamos utilizar a igualdade [tex]x=r^2\,.[/tex] Mas perceba que [tex]r^2 \gt 1[/tex] e [tex]x_2 \lt 0[/tex]; assim descartaremos essa solução. Dessa forma ficamos, apenas, com [tex]x_1=r^2\,[/tex], donde segue que:
[tex]\qquad \dfrac{1+\sqrt{5}}{2}=r^2[/tex]
[tex]\qquad \sqrt{r^2}=\sqrt{\dfrac{1+\sqrt{5}}{2}}\\
\,[/tex]
[tex]\qquad\left|\,r \,\right|=\sqrt{\dfrac{1+\sqrt{5}}{2}}\\
\,[/tex]
[tex]\qquad\ r=\pm \sqrt{\dfrac{1+\sqrt{5}}{2}}\,[/tex].
Para finalizar, observe que [tex]r\gt 0 [/tex], assim descartamos o valor [tex] r=- \sqrt{\dfrac{1+\sqrt{5}}{2}}[/tex] e, portanto, a razão da progressão que satisfaz o problema é [tex]\, \fcolorbox{black}{#eee0e5}{$\, r= \sqrt{\dfrac{1+\sqrt{5}}{2}}\,$}\,.[/tex]
Observação: Particularmente, observe que [tex] r=\sqrt{\dfrac{1+\sqrt{5}}{2}}\approx 1,27[/tex]; logo, [tex]r \gt 1\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
|
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |