✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
As circunferências de centro [tex]C_1[/tex] e [tex]C_2[/tex] mostradas na figura têm raios com comprimentos [tex]3\, \text{cm}[/tex] e [tex]5\, \text{cm}[/tex], respectivamente, são tangentes exteriores e as retas tangentes a ambas se intersectam no ponto [tex]P.[/tex]
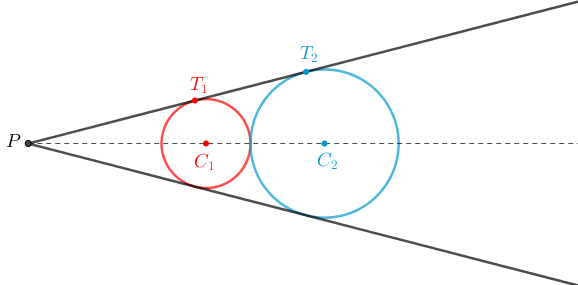
Observando que os pontos [tex]P[/tex], [tex]C_1[/tex] e [tex]C_2[/tex] são colineares, calcule a distância entre os pontos de tangência [tex]T_1[/tex] e [tex]T_2.[/tex]

Lembretes
(1) Caso de Semelhança A.A. (ângulo – ângulo): Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes.
(2) Em triângulos semelhantes, os lados correspondentes são proporcionais.
(Há uma Sala de Ajuda sobre triângulos semelhantes no nosso Blog!)
(3) Uma reta tangente a uma circunferência é perpendicular ao raio no seu ponto de tangência.
(4) Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
Solução
Como [tex]T_1[/tex] e [tex]T_2[/tex] são pontos de tangência das circunferências de centro [tex]C_1[/tex] e [tex]C_2[/tex], respectivamente, então os segmentos [tex]C_1T_1[/tex] e [tex]C_2T_2[/tex] são perpendiculares à reta [tex]T_1T_2[/tex].
Dessa forma, os triângulos retângulos [tex]\Delta PT_1C_1[/tex] e [tex]\Delta PT_2C_2[/tex] são semelhantes, já que têm um ângulo reto cada e o ângulo [tex]C_2\hat{P}T_2[/tex] é comum aos dois triângulos.
Na nossa discussão denotaremos por [tex]A[/tex] o ponto de interseção da reta [tex]PC_1[/tex] com a circunferência de centro [tex]C_1[/tex] e por [tex]x[/tex] o comprimento do segmento [tex]PA[/tex].
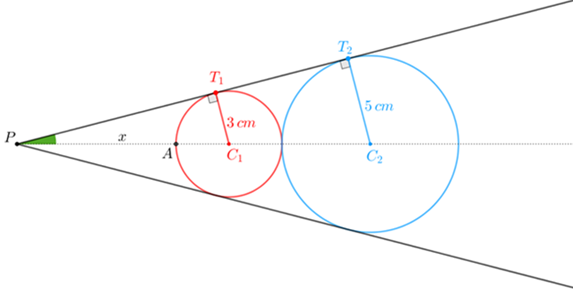
Como [tex]\Delta PT_1C_1[/tex] e [tex]\Delta PT_2C_2[/tex] são triângulos semelhantes, então podemos utilizar o Lembrete 2 e concluir que:
[tex]\qquad \qquad \dfrac{5}{3}=\dfrac{x+11}{x+3}[/tex]
[tex]\qquad \qquad 5(x+3)=3(x+11)[/tex]
[tex]\qquad \qquad 5x+15=3x+33[/tex]
[tex]\qquad \qquad 2x=18[/tex]
[tex]\qquad \qquad \boxed{x=9}[/tex] .
Com o valor de [tex]x[/tex], obtemos as hipotenusas dos triângulos [tex]\Delta PT_1C_1[/tex] e [tex]\Delta PT_2C_2[/tex]; vamos calcular os respectivos segundos catetos, para poder obter a distância entre os pontos [tex]T_1[/tex] e [tex]T_2.[/tex]
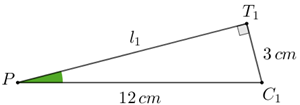
Pelo Teorema de Pitágoras, obtemos que: |
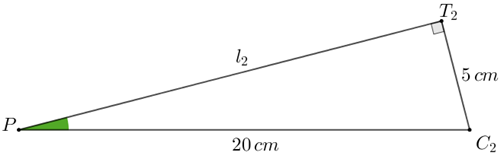
Pelo Teorema de Pitágoras, obtemos que: |
Com esses dados estamos prontos para calcular a distância entre os pontos de tangência, a qual denotaremos por [tex]d[/tex]:
[tex]\qquad \qquad d=\sqrt{375}-\sqrt{135}\approx 19,36-11,62.[/tex]
(Cuidado, [tex]\sqrt{375}-\sqrt{135} \ne \sqrt{375-135}.[/tex])

► Portanto, a distância entre os pontos de tangência [tex]T_1[/tex] e [tex]T_2[/tex] é aproximadamente [tex] \, \fcolorbox{black}
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
