✏ Link do problema para dispositivos da Apple.
Problema
Uma pessoa parte do ponto A e chega no ponto B da malha quadriculada mostrada na figura abaixo.
Ela se move apenas sobre as linhas da malha e nunca repete um lugar pelo qual ela já passou.
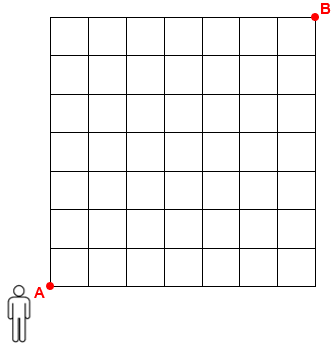
Além disso, os únicos movimentos permitidos são para baixo, para cima e para a direita, mas NÃO para a esquerda.
Um caminho possível é mostrado na figura abaixo.
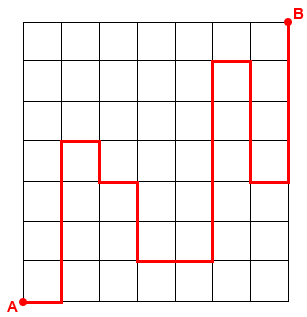
Calcule o número total de maneiras que essa pessoa pode ir do ponto A ao ponto B, seguindo as regras estabelecidas.

Ajuda
✏ Princípio Fundamental da Contagem, ou Princípio Multiplicativo: Se
- uma decisão D1 puder ser tomada de [tex] m_1 [/tex] maneiras distintas,
- uma decisão D2 puder ser tomada de [tex] m_2 [/tex] maneiras distintas,
- [tex]\cdots[/tex]
- uma decisão Dk puder ser tomada de [tex]m_k [/tex] maneiras distintas,
- e todas essas decisões forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha de outra),
então o número total de maneiras de tomarmos sucessivamente essas [tex]k[/tex] decisões é igual ao produto
[tex]\qquad \qquad \boxed{m_1\times m_2 \times \cdots \times m_k}\, .[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
Solução
- Perceba que, como a pessoa não pode ir para a esquerda, para ela sair do ponto A e chegar no ponto B, ela deve se deslocar sete vezes para a direita.
- Mas a pessoa não pode passar duas vezes pelo mesmo lugar; então, a partir de qualquer ponto em que ela esteja na malha, ela pode ir para a direita de oito modos diferentes, subindo ou descendo antes pela linha vertical na qual ela se encontra. Veja um exemplo dessa afirmação na imagem a seguir.
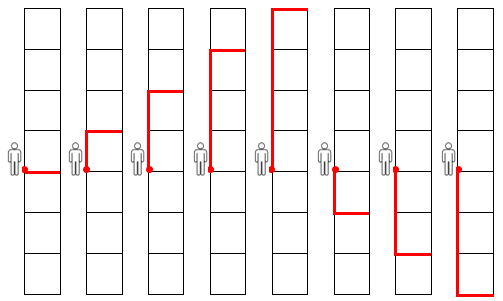
Portanto, pelo Princípio Fundamental da Contagem, o número total de maneiras que essa pessoa pode ir do ponto A ao ponto B, de acordo com as regras estabelecidas, é dado pelo produto
[tex]\qquad \qquad 8\times 8\times 8\times 8\times 8\times 8\times 8= 8^7= \fcolorbox{black}{#FFCCD0}{$2\;097\;152$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Nível B – Questão Mediana
