Problema
(Indicado a partir do 9º ano do E. F.)
Para evitar que duas árvores verticais vizinhas caiam sobre uma pista e causem acidentes, a Autarquia de Manutenção e Limpeza Urbana de uma determinada cidade utilizará cabos de sustentação de uma árvore a outra, conforme indicado na figura a seguir.
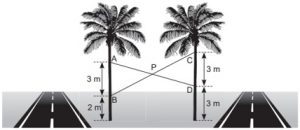
Sabe-se que as alturas de instalação dos cabos indicadas na figura foram especificadas seguindo as recomendações previstas pela prefeitura da cidade. Se os cabos forem instalados conforme as alturas especificadas, qual será a altura, em metros, do ponto de interseção dos cabos em relação ao solo?
Extraído de Simulado SAS.

Lembretes
(1) Se duas retas paralelas são intersectadas por uma transversal, então os pares de ângulos alternos internos que essa transversal define são congruentes. (Precisa relembrar estes conceitos? Dê uma passadinha nesta Sala.)
(2) Caso de Congruência A.L.A. (ângulo – lado – ângulo): Se dois triângulos têm congruentes dois ângulos e o lado compreendido por eles, então estes triângulos são congruentes.
(Há uma Sala para leitura sobre triângulos congruentes no nosso Blog!)
(3) Em triângulos semelhantes, os lados correspondentes são proporcionais.
(Há uma Sala de Ajuda sobre triângulos semelhantes no nosso Blog!)
Solução
Perceba que, como as árvores são verticais, podemos identificar dois pares de ângulos alternos internos [tex]P\hat{A}B[/tex] com [tex]P\hat{D}C[/tex] e [tex]P\hat{B}A[/tex] com [tex]P\hat{C}D[/tex]).
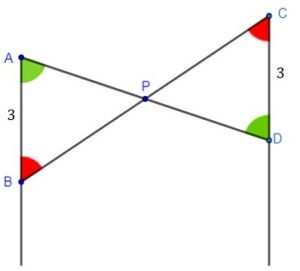
Como [tex]AB=CD=3[/tex], pelo caso A.L.A. (ângulo-lado-ângulo), concluímos que os triângulos [tex]APB[/tex] e [tex]DPC[/tex] são congruentes. Assim, [tex]BP=PC[/tex]. Chamemos de [tex]x[/tex] a altura, em metros, do ponto [tex]P[/tex] em relação ao solo.
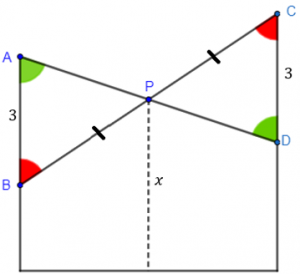
Dessa forma, ao traçar uma reta paralela ao solo passando pelo ponto [tex]B[/tex], conclui-se, pela semelhança entre os triângulos [tex]BRP[/tex] e [tex]BSC[/tex] que:
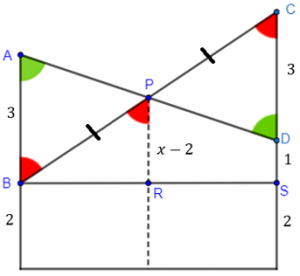
Portanto, a distância do ponto [tex]P[/tex] ao solo será de [tex]4[/tex] metros.
Solução elaborada pelos Moderadores do Blog.
