Dedução 3
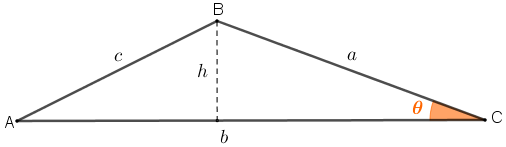
Sejam [tex]a, b[/tex] e [tex]c[/tex] os comprimentos dos lados de um triângulo [tex]ABC[/tex], sendo que o vértice [tex]B[/tex] é o que define o ângulo interno com a maior medida, e seja [tex]h[/tex] a medida da altura do triângulo [tex]ABC[/tex], relativa a esse vértice. Veja a figura ao lado.
Sabemos que a área de um triângulo é dada por [tex]\dfrac{base \times altura}{2}[/tex].
Assim, se [tex]A_t[/tex] é a área do triângulo [tex]ABC[/tex], então particularmente temos que:
[tex]\qquad \qquad A_t=\dfrac{b\times h}{2}. \qquad \textcolor{#800000}{(i)}[/tex]
Vamos procurar uma expressão para [tex]h[/tex], a partir dos comprimentos [tex]a, b[/tex] e [tex]c.[/tex]
Observe que, utilizando a definição do seno de um determinado ângulo, obtemos que [tex]sen\, \theta=\dfrac{h}{a}[/tex], ou seja, [tex]h=a\,sen\, \theta.[/tex] Dessa forma, podemos reescrever a igualdade [tex] \textcolor{#800000}{(i)}[/tex] da seguinte forma:
[tex]\qquad \qquad A_t=\dfrac{ab}{2}sen\, \theta. \qquad \textcolor{#800000}{(ii)}[/tex]
Vejamos, agora, o que fazer com o [tex]sen\, \theta\, .[/tex]
Note que:
- pela Lei Fundamental da Trigonometria, temos que [tex]sen^2\,\theta +cos^2\,\theta=1[/tex] e, assim, [tex]\boxed{sen^2\,\theta=1-cos^2\,\theta}\, [/tex];
- pela Lei dos Cossenos, temos que [tex]c^2=a^2+b^2-2ab\, cos\,\theta\, [/tex] e, assim, [tex]\boxed{cos\,\theta=\dfrac{a^2+b^2-c^2}{2ab}}[/tex].
Portanto, [tex]sen^2\,\theta=1-\left({\dfrac{a^2+b^2-c^2}{2ab}}\right)^2.[/tex] Vamos desenvolver algebricamente essa igualdade e para isso vamos utilizar seguidamente dois produtos notáveis:
- [tex]x^2-y^2=(x-y)\cdot (x+y), \forall\, \, x,y \in \mathbb{R};\qquad \textcolor{#800000}{(iii)}[/tex]
- [tex](x\pm y)^2=x^2 \pm 2xy+y^2, \forall\, \, x,y \in \mathbb{R}.\qquad \textcolor{#800000}{(iv)}[/tex]
Vamos lá:
[tex]\qquad \begin{align*}sen^2\,\theta&=1-\left({\dfrac{a^2+b^2-c^2}{2ab}}\right)^2\\
&=1-\dfrac{\left(a^2+b^2-c^2\right)^2}{4a^2b^2}\\
&=\dfrac{4a^2b^2-\left(a^2+b^2-c^2\right)^2}{4a^2b^2}\\
&=\dfrac{1}{4a^2b^2}\left[(2ab)^2-\left(a^2+b^2-c^2\right)^2\right]\\
&\stackrel{\textcolor{#800000}{(iii)}}{=}\dfrac{1}{4a^2b^2}\left[\left(\textcolor{red}{(2ab)-\left(a^2+b^2-c^2\right)}\right)\cdot \left(\textcolor{blue}{(2ab)+\left(a^2+b^2-c^2\right)}\right)\right]\\
&=\dfrac{1}{4a^2b^2}\left[\left(\textcolor{red}{2ab-a^2-b^2+c^2}\right)\cdot \left(\textcolor{blue}{2ab+a^2+b^2-c^2}\right)\right]\\
&=\dfrac{1}{4a^2b^2}\left[\left(\textcolor{red}{c^2-(a^2-2ab+b^2)}\right)\cdot \left(\textcolor{blue}{(a^2+2ab+b^2)-c^2}\right)\right]\\
&\stackrel{\textcolor{#800000}{(iv)}}{=}\dfrac{1}{4a^2b^2}\left[\left(\textcolor{red}{c^2-(a-b)^2}\right)\cdot \left(\textcolor{blue}{(a+b)^2-c^2}\right)\right]\\
&\stackrel{\textcolor{#800000}{(iii)}}{=}\dfrac{1}{4a^2b^2}\left[\left(\textcolor{red}{(c-(a-b)) \cdot (c+(a-b))}\right)\cdot \left(\textcolor{blue}{((a+b)-c) \cdot ((a+b)+c)}\right)\right]\\
&=\dfrac{1}{4a^2b^2}\left[\left(\textcolor{red}{(c-a+b) \cdot (c+a-b)}\right)\cdot \left(\textcolor{blue}{(a+b-c) \cdot (a+b+c)}\right)\right].\qquad \textcolor{#800000}{(v)}\\
\end{align*}[/tex]
Veja que, se [tex]\boxed{p=\dfrac{a+b+c}{2}}[/tex], então [tex]2p=a+b+c[/tex] e com isso:
- [tex]c+b=2p-a[/tex], donde [tex]\boxed{c-a+b}=(c+b)-a=(2p-a)-a={2p-2a}[/tex],
- [tex]c+a=2p-b[/tex], donde [tex]\boxed{c+a-b}=(c+a)-b=(2p-b)-b={2p-2b}[/tex],
- [tex]a+b=2p-c[/tex], donde [tex]\boxed{a+b-c}=(a+b)-c=(2p-c)-c={2p-2c}[/tex].
Logo, segue de [tex] \textcolor{#800000}{(v)}[/tex] que:
[tex]\qquad sen^2\,\theta=\dfrac{1}{4a^2b^2}\left[\left((2p-2a) \cdot (2p-2b)\right)\cdot \left((2p-2c) \cdot (2p)\right)\right][/tex]
[tex]\qquad sen^2\,\theta=\dfrac{1}{4a^2b^2}\left[2(p-a) \cdot 2(p-b)\cdot 2(p-c) \cdot (2p)\right]\\
\qquad sen^2\,\theta=\dfrac{16}{4a^2b^2}\left[p \cdot(p-a) \cdot (p-b)\cdot (p-c) \right]\\
\qquad sen^2\,\theta=\dfrac{4}{a^2b^2}\left[p \cdot(p-a) \cdot (p-b)\cdot (p-c) \right].[/tex]
Sendo [tex]a,\, b,sen\, \theta \gt 0[/tex], podemos concluir que
[tex]\qquad sen\theta=\sqrt{\dfrac{4}{a^2b^2}\left[p \cdot(p-a) \cdot (p-b)\cdot (p-c) \right]}\\
\qquad sen\theta=\dfrac{2}{ab}\sqrt{p \cdot(p-a) \cdot (p-b)\cdot (p-c) }\\[/tex]
donde, por [tex] \textcolor{#800000}{(ii)}[/tex], temos que
[tex]\qquad \qquad A_t=\dfrac{ab}{2}sen\, \theta\\
\qquad \qquad A_t=\dfrac{ab}{2}\left(\dfrac{2}{ab}\sqrt{p \cdot(p-a) \cdot (p-b)\cdot (p-c)}\right)\\
\qquad \qquad A_t=\dfrac{\cancel{ab}}{\bcancel{2}}\left(\dfrac{\bcancel{2}}{\cancel{ab}}\sqrt{p \cdot(p-a) \cdot (p-b)\cdot (p-c)}\right)[/tex]
[tex]\qquad \qquad \, \fcolorbox{black}{#eee5de}{$A_t=\sqrt{p \cdot (p-a) \cdot (p-b) \cdot (p-c)}$}\, [/tex], que é a fórmula de Herão.
Equipe COM – OBMEP
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
