Aplicando a matemática básica – Sala 1

Porcentagem

A porcentagem, simbolizada por [tex]\%[/tex], é uma ferramenta muito utilizada quando nos referimos, principalmente, a atrativos comerciais.

É um conceito muito importante, pois invade o comércio sob diversas formas e idiomas diferentes.

A porcentagem sempre está presente expressando desconto ou aumento, quer seja para antecipar uma parcela de um financiamento ou mesmo para calcular a multa devida ao atraso de alguma prestação. Sem o conhecimento básico desse assunto, as pessoas podem cair em algumas “armadilhas”.

Entendeu? O que você escolheria?
Pois é! É necessário ter um mínimo de conhecimento em porcentagem.

Pense um pouco e mais tarde voltaremos a essa pergunta.

A porcentagem apresenta estreitas ligações com a ideia de fração, já que porcentagem pode ser definida como uma razão na forma [tex]\dfrac{a}{100}[/tex], na qual [tex]a[/tex] é um número real. Essa razão é comumente escrita na forma [tex]a\%[/tex] (Leitura: [tex]a[/tex] por cento, isto é, “[tex]a [/tex] por cem”).
Particularmente, a fração [tex]\dfrac{1}{100}[/tex] (a centésima parte de um todo, ou seja, uma das cem partes nas quais um todo foi dividido) é denotada por [tex] 1\%[/tex] (um por cento, isto é, “um por cem”).
Portanto, [tex]\fcolorbox{black}{#d4ccbe}{$1\%=\dfrac{1}{100}=0,01$}[/tex].

Nesta altura do campeonato, alguém pode estar se perguntando: mas qual é a vantagem de se utilizar porcentagem, já que podemos utilizar simplesmente frações?

Terminadas as eleições deste ano, foi divulgada a relação dos quatro vereadores eleitos mais votados de uma determinada região.
Observando que esses quatro vereadores não foram eleitos em um mesmo município, necessariamente, proporcionalmente qual foi o mais votado da região?
Talvez fosse mais fácil responder a essa pergunta se o resultado da votação fosse divulgado da maneira abaixo, não é?

Tá certo que a mera apresentação de frações com o mesmo denominador já ajuda na comparação de razões; mas, mostrando por uma porcentagem o que uma dada fração representa em um grupo de 100 coisas, muitas vezes fica mais claro para quem não é da área da Matemática, pois o valor representativo comparativo dá uma boa noção de comparação. Veja, por exemplo, que [tex]15\%[/tex] de um grupo de [tex]100[/tex] alunos parece ser mais fácil de calcular que [tex]15\%[/tex] de um grupo de [tex]67[/tex] alunos. Quando falamos que uma quantidade representa [tex]50\%[/tex] de outra quantidade, já temos uma ideia de metade, posto que o todo é [tex]100\%[/tex]. Quando falamos que algo representa [tex]40\%[/tex] ou [tex]45\%[/tex], sabemos que é um pouco menos que a metade, e assim por diante. E como [tex]100\%=\dfrac{100}{100}=1[/tex], dizemos que [tex]100\%[/tex] é o “nosso todo”.
Matematicamente, a porcentagem pode ser representada de três maneiras diferentes: um número com o símbolo [tex]\%[/tex]; na forma de razão, com o denominador [tex]100[/tex]; ou como um número decimal. Assim:

[tex] \, 30\%[/tex] é o mesmo que [tex]\dfrac{30}{100}[/tex], ou [tex]0,30[/tex] na forma decimal;
[tex]120\%[/tex] é o mesmo que [tex]\dfrac{120}{100}[/tex], ou [tex]1,20[/tex] na forma decimal;
[tex]200\%[/tex] é o mesmo que [tex]\dfrac{200}{100}[/tex], ou [tex]2,00[/tex] na forma decimal;
[tex] \, 20\%[/tex] é o mesmo que [tex]\dfrac{20}{100}[/tex], ou [tex]0,20[/tex] na forma decimal;
[tex] \, \, \, 2\%[/tex] é o mesmo que [tex]\dfrac{2}{100}[/tex], ou [tex]0,02[/tex] na forma decimal;

mas, dependendo do contexto, a porcentagem escrita na forma de razão é chamada de taxa percentual.

Saber efetuar cálculos de porcentagem é fundamental, uma vez que, de promoções a financiamentos, diariamente nos deparamos com situações que requerem utilização de porcentagem. Muitas dessas situações podem ser resolvidas a partir de três “situações básicas”, cujas respectivas soluções envolvem tão somente uma regra de três simples:
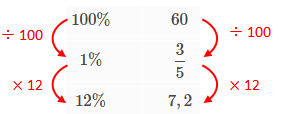
[tex](i)[/tex] conhecemos o valor total (o que corresponde a [tex]100\%[/tex]) e queremos o valor correspondente a uma porcentagem desse total;
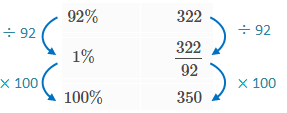
[tex](ii)[/tex] conhecemos o valor correspondente a uma porcentagem do total e queremos esse valor total (o que corresponde a [tex]100\%[/tex]);
[tex](iii)[/tex] conhecemos, respectivamente, os valores correspondentes ao todo e a uma porcentagem desse todo e queremos a porcentagem ([tex]p\%[/tex]).

Cliquem no botão abaixo e vejam exemplos
que ilustram como utilizar Regra de três nessas situações.

Os próximos exemplos ilustrarão como utilizar regra de três nas situações [tex](i)[/tex], [tex](ii)[/tex] e [tex](iii)[/tex].

Exemplo 1: Em uma promoção, uma camiseta que custa [tex]60[/tex] reais está sendo vendida com [tex]12\%[/tex] de desconto. Se eu aproveitar a oferta, de quantos reais será a economia que farei?

Resolução:
Deparamo-nos com a situação [tex](i)[/tex], já que nos é dado o todo, [tex]60[/tex] reais, e desse todo queremos uma porcentagem,[tex]12\%[/tex]. De outra forma, se [tex]R\$ \, 60[/tex] correspondem a [tex]100\%[/tex], quantos reais corresponderão a [tex]12\%[/tex]? Se denotarmos tal quantidade de reais por [tex]r[/tex], esquematicamente teremos:

[tex]60[/tex] reais	————————————–	[tex]100\%[/tex]
[tex]r[/tex] reais	————————————–	[tex]12\%[/tex]

“Armando” a nossa regra de três simples, temos que [tex]60\times 12= r \times 100[/tex].
Fazendo as contas:
[tex]\qquad \qquad r=\dfrac{60\times 12}{100}=7,2[/tex].
Assim, se eu aproveitar a oferta, farei uma economia de [tex]R\$ \, 7,20[/tex] na compra de uma camiseta!

Observação: Se vocês não sabem “Regra de três”, não faz mal; basta raciocinar assim:

Se a [tex]\qquad 100\%[/tex] corresponde [tex]60[/tex] reais, então a [tex]\qquad 1\%[/tex] corresponderá [tex]\dfrac{60}{100}=\dfrac{3}{5}[/tex] reais. Assim, a [tex]\qquad 12\%[/tex] corresponderá [tex]12 \times 1\%[/tex], ou seja, [tex]\qquad 12 \times \dfrac{3}{5}=\dfrac{36}{5}=7,2[/tex] reais.

Exemplo 2: Devido ao mau tempo, a empresa de aviação “Voa Alto” precisou cancelar um de seus voos. Até este momento, a empresa já conseguir acomodar [tex]322[/tex] passageiros, o que corresponde a [tex]92\%[/tex] dos passageiros desse voo. Assim, qual o total de passageiros do voo cancelado?

Resolução:
Aqui temos a situação [tex](ii)[/tex], uma vez que sabemos que [tex]92\%[/tex] de um total correspondem a [tex]322[/tex] passageiros e queremos calcular o total de passageiros. Assim, como [tex]322[/tex] passageiros correspondem a [tex]92\%[/tex], quantos passageiros corresponderão a [tex]100\%[/tex]? Se denotarmos tal quantidade de passageiros por [tex]n[/tex], esquematicamente teremos:

[tex]322[/tex] passageiros	————————————–	[tex]92\%[/tex]
[tex]n[/tex] passageiros	————————————–	[tex]100\%[/tex]

“Armando” essa segunda regra de três simples, teremos que [tex]322\times 100= n \times 92[/tex].
Fazendo as contas:
[tex]\qquad \qquad n=\dfrac{322\times 100}{92}=350[/tex],
e, assim, o total de passageiros do voo cancelado pela empresa “Voa alto” é [tex]350[/tex].

Observação: Para resolver o problema sem a utilização de “Regra de três”, basta raciocinar assim:

Se a [tex]\qquad 92\%[/tex] corresponde [tex]322[/tex] passageiros, então a [tex]\qquad 1\%[/tex] corresponderá [tex]\dfrac{322}{92}[/tex] passageiros. Logo, a [tex]\qquad 100\%[/tex] corresponderá [tex]100\times 1\%[/tex], ou seja, [tex]\quad 100 \times \dfrac{322}{92}=\dfrac{32200}{92}=350[/tex] passageiros.

Exemplo 3: Na partida inaugural do estádio de um time de futebol compareceram [tex]36.080[/tex] torcedores. Se a capacidade total do novo estádio é de [tex]41.000[/tex] torcedores, qual foi a porcentagem de ocupação do estádio nessa partida?

Resolução:
Neste caso, temos a situação [tex](iii)[/tex], já que conhecemos a capacidade total do estádio, [tex]41.000[/tex] torcedores, sabemos que o número de torcedores que assistiram à partida inaugural foi de [tex]36.080[/tex] e queremos a porcentagem de ocupação do estádio nesse dia. Se denotarmos esse percentual por [tex] p\%[/tex], teremos que:

[tex]41.000[/tex] torcedores	————————————–	[tex]100\%[/tex]
[tex]36.080[/tex] torcedores	————————————–	[tex]p\%[/tex]

Assim, teremos que [tex]36080\times 100= p \times 41000[/tex], donde:

[tex]\qquad \qquad p=\dfrac{36080\times 100}{41000}=\dfrac{3608}{41}=88[/tex].

Como [tex]p=88[/tex], a porcentagem [tex]p\%[/tex] de ocupação do estádio na partida inaugural foi de [tex]88\%[/tex].

Lembrando que [tex]100\%[/tex] é o todo, poderíamos pensar que estamos interessados em saber quanto [tex]36.080[/tex] representa do todo:

[tex]41.000[/tex] torcedores	————————————–	[tex]1[/tex]
[tex]36.080[/tex] torcedores	————————————–	[tex]r[/tex]

e então, [tex]41000 \, r=36080[/tex], donde:

[tex]\qquad \qquad r=\dfrac{36080}{41000}=\dfrac{3608}{4100}=0,88=\dfrac{88}{100}=88\%[/tex].

Observação: Para resolver o problema sem a utilização de “Regra de três”, basta lembrar a definição de porcentagem:

Percebam que os [tex]41.000[/tex] torcedores correspondem a [tex]100\%[/tex], assim queremos saber “quantos por cento” [tex]36.080[/tex] representa de [tex]41.000[/tex] e, portanto, basta encontrar uma fração com denominador [tex]100[/tex] que seja equivalente à [tex]\dfrac{36080}{41000}:[/tex] [tex]\qquad \dfrac{3608}{4100}= 0,88=\dfrac{88}{100}=88\%[/tex]

➤ Uma primeira situação prática de aplicação de porcentagem.

➤ Um exemplo bastante interessante.

➤ Podemos explorar um pouco mais situações como a do exemplo anterior e lembrar que:

➤ E nas situações onde estão envolvidos aumentos e descontos?
Será que a ordem na qual as operações são feitas influenciará o resultado final?
Vamos ver…

➤ Você sabe como calcular porcentagem usando a calculadora?

Entendeu porque é necessário saber operar com porcentagens?
Esse é um assunto da Matemática que é aplicado em
todos os ramos do conhecimento humano.

Equipe COM – OBMEP