✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Muito Difícil)
Determinar os dois valores de [tex]x[/tex] mais próximos a [tex]2003^{\circ}[/tex] (por falta e por excesso) que cumprem a seguinte equação trigonométrica:
[tex]\quad \qquad \dfrac{1}{sen^2x}-\dfrac{1}{cos^2x}-\dfrac{1}{tg^2x}-\dfrac{1}{cotg^2x}-\dfrac{1}{sec^2x}-\dfrac{1}{cossec^2x}=-3[/tex].
Solução
- Utilizando definições básicas da trigonometria,
[tex]\begin{array}{c c c c c c c c c c }
\textcolor{red}{\dfrac{1}{sen^2x}} & & \textcolor{blue}{\dfrac{1}{cos^2x}} & & \textcolor{green}{\dfrac{1}{tg^2x}} & & \textcolor{#FF8C00}{\dfrac{1}{cotg^2x}} & & \textcolor{#9400D3}{\dfrac{1}{sec^2x}} & & \textcolor{#8B7355}{\dfrac{1}{cossec^2x}} \\
\downarrow & & \downarrow & & \downarrow & & \downarrow & & \downarrow & & \downarrow \\
\textcolor{red}{cossec^2x} & & \textcolor{blue}{sec^2x} & & \textcolor{green}{cotg^2x} & & \textcolor{#FF8C00}{tg^2x} & & \textcolor{#9400D3}{cos^2x} & & \textcolor{#8B7355}{sen^2x} \end{array} \, \, [/tex],
- podemos reescrever a igualdade dada no problema da seguinte forma:
[tex]\quad \boxed{ cossec^2x-sec^2x-cotg^2x-tg^2x-cos^2x-sen^2x=-3} \, .[/tex]
- Perceba agora que podemos utilizar relações fundamentais da trigonometria e reescrever a equação obtida a partir, apenas, de tangentes e cotangentes:
[tex]\quad \qquad cossec^2x-sec^2x-cotg^2x-tg^2x-cos^2x-sen^2x=-3[/tex]
[tex]\quad \qquad \textcolor{red}{cossec^2x}-\textcolor{blue}{sec^2x}-cotg^2x-tg^2x-\textcolor{green}{\left(cos^2x+sen^2x\right)}=-3[/tex]
[tex]\quad \qquad \textcolor{red}{\left(1+cotg^2x\right)}-\textcolor{blue}{\left(1+tg^2x\right)}-cotg^2x-tg^2x-\textcolor{green}{1}=-3[/tex]
- Fazendo as simplificações possíveis na última igualdade, obtemos uma equação trigonométrica relativamente simples. Observe:
[tex]\qquad \left(1+cotg^2x\right)-\left(1+tg^2x\right)-cotg^2x-tg^2x-1=-3[/tex]
[tex]\qquad 1+cotg^2x-1-tg^2x-cotg^2x-tg^2x-1=-3[/tex]
[tex]\qquad \bcancel{1}+\cancel{cotg^2x}-\bcancel{1}-tg^2x-\cancel{cotg^2x}-tg^2x-1=-3[/tex]
[tex]\qquad -tg^2x-tg^2x-1=-3[/tex]
[tex]\qquad 2tg^2x=2[/tex]
[tex]\qquad \boxed{tg^2x=1} \, .[/tex]
Mudamos nosso foco; agora temos que resolver a equação [tex]\boxed{tg^2x=1} \, .[/tex]
- Algebricamente, temos que:
[tex]\qquad tg^2x=1 \, [/tex]
[tex]\qquad \sqrt{tg^2x}=\sqrt{1} \, [/tex]
[tex]\qquad \sqrt{\left(tg\,x\right)^2}=1 \, [/tex]
[tex]\qquad |tg\,x|=1 \, [/tex]
[tex]\qquad tg\,x=\pm 1 \, .\qquad \textcolor{#800000}{(i)}[/tex]
Voltemos à Trigonometria…
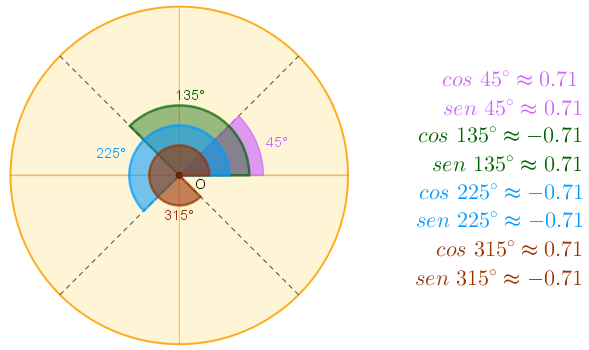
Sabemos que [tex]tg\,x=\dfrac{sen\,x}{cos\,x}[/tex]; assim, como [tex]tg\,x=\pm1[/tex], então [tex]sen\,x=\pm cos\,x[/tex], ou seja, estamos procurando ângulos cujos respectivos senos e cossenos são iguais ou diferem apenas por sinal. Consultando uma tabela trigonométrica, uma calculadora científica ou o quadro abaixo, verificamos rapidamente que [tex]tg \, 45^\circ=1[/tex], então [tex]\theta=45^\circ[/tex] é um dos infinitos ângulos que satisfazem a equação [tex]\textcolor{#800000}{(i)}[/tex].
Olhando o círculo trigonométrico, percebemos quatro ângulos que satisfazem [tex]\textcolor{#800000}{(i)}[/tex]: [tex] \, \theta_1=45^\circ[/tex] ; [tex]\theta_2=135^\circ[/tex] ; [tex]\theta_3=225^\circ[/tex] e [tex]\theta_4=315^\circ.[/tex]
A solução geral da equação [tex]\textcolor{#800000}{(i)}[/tex] é dada por [tex]\fcolorbox{black}{#eee0e5}{$x=45^\circ+90^\circ k$} \, [/tex], com [tex]k \in \mathbb{Z}[/tex], mas queremos as soluções mais próximas ao valor [tex]2003^\circ[/tex]. Dessa forma, deveremos encontrar números inteiros [tex]k_1[/tex] e [tex]k_2[/tex] tais que [tex]\boxed{45^\circ+90^\circ k_1 \leqslant 2003^\circ \leqslant 45^\circ+90^\circ k_2}[/tex]; vamos lá:
[tex]\qquad 45^\circ+90^\circ k_1 \leqslant 2003^\circ \leqslant 45^\circ+90^\circ k_2[/tex]
[tex]\qquad 90^\circ k_1 \leqslant 1958^\circ \leqslant 90^\circ k_2[/tex]
[tex]\qquad k_1 \leqslant \dfrac{1958^\circ}{90^\circ} \leqslant k_2[/tex]
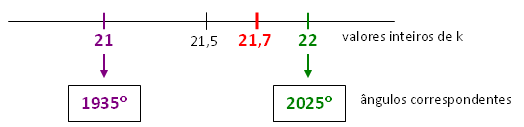
[tex]\qquad k_1 \leqslant 21,7 \leqslant k_2.[/tex]
Portanto, os valores inteiros em questão são [tex]k_1=21 \, [/tex] e [tex] \, k_2=22[/tex] e os valores solicitados no problema são [tex]\fcolorbox{black}{#eee0e5}{$1935^\circ$} \, [/tex] e [tex]\fcolorbox{black}{#eee0e5}{$2025^\circ$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
