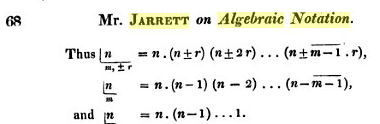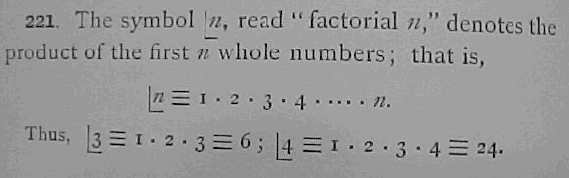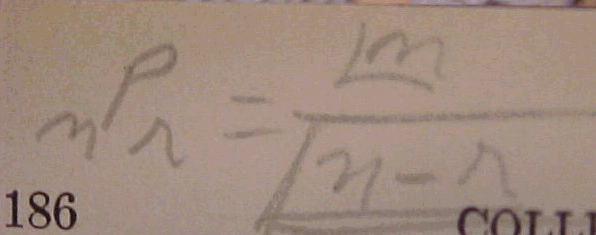Sala para leitura_009: Fatorial e Permutação Simples

Perguntas como a apresentada acima podem ser encontradas com muita frequência no nosso cotidiano; e, em geral, pelo Princípio Fundamental da Contagem (PFC), também chamado de Princípio Multiplicativo, a resposta a esse tipo de problema é imediata.

No caso do problema formulado, há 5 possibilidades para escolhermos a pessoa que utilizará o primeiro computador. Escolhida tal pessoa, há 4 possibilidades para aquela que ocupará o segundo computador.
Seguindo esse raciocínio, é muito simples perceber que, utilizando o PFC, a resposta ao problema será:
5 ⋅ 4 ⋅ 3⋅ 2 ⋅ 1 = 120.

Imagine, porém, que o problema inicial se referisse a 100 funcionários do Call Center de uma importante empresa que fossem fazer um treinamento em uma gigantesca sala de computação, com 100 computadores. Será que, para registrarmos a solução, precisaríamos escrever o correspondente produto com cem fatores???
Com certeza não precisaríamos escrever todos os cem fatores e nem mesmo expressões com uso de reticências, como, por exemplo, 100 ⋅ 99 ⋅ 98 ⋅ . . . ⋅ 2 ⋅ 1. Explicitar produtos como esse toda vez que eles aparecerem é algo desnecessário, já que o matemático francês Christian Kramp (Conheça um pouco do trabalho desse matemático aqui.) decidiu adotar uma notação muito simples para produtos desse tipo:  ele decidiu representar o fatorial do número [tex]n[/tex] por [tex]n.
– Elegante, não é?
Porém, esta notação não foi a única utilizada para representar o fatorial de um número natural. Para conhecer um pouco dessa história, clique no botão abaixo.

Pois agora que já viajamos um pouco pela história do fatorial, vamos conferir alguns exemplos? Observe:
      4! = 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24;
      10! = 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 3628800
      n! = n ⋅ (n – 1) ⋅ (n – 2) ⋅ … ⋅ 3 ⋅ 2 ⋅ 1.

De uma maneira mais formal, o fatorial de um número natural [tex]n[/tex] é o número denotado por [tex]n![/tex] e definido da seguinte forma:

  • [tex]n!=1[/tex], se [tex]n=0[/tex];
  • [tex]n!=n \cdot (n-1)![/tex], se [tex]n\gt 0[/tex].

A atenção e o cuidado na hora de trabalhar com fatoriais é muito importante. A soma a! + b! ou o produto a! ⋅ b! , por exemplo, não são equivalentes a (a + b)! ou a (a ⋅ b)! (tente entender o porquê!).
Uma interessante propriedade dos fatoriais é a de que, se [tex]a[/tex] e [tex]b[/tex] forem números naturais, com [tex]a\gt b[/tex], então
[tex] \qquad\qquad \dfrac{a!}{b!} = a(a-1)(a-2)\cdot \, \cdots \, \cdot(b+1)[/tex]
ou, de forma equivalente,
[tex]\qquad\qquad a!=a(a-1)(a-2)\cdot \, \cdots \, \cdot(b+1)\cdot b! [/tex].
Que tal tentar provar essas igualdades?
Elas facilitam bastante cálculos que envolvam fatoriais. De acordo com elas, nós temos, por exemplo, [tex]\dfrac{10!}{9!} = 10[/tex] e [tex]\dfrac{50!}{47!} = 50\cdot 49\cdot 48 = 117600[/tex]. Por que isso ocorre?

Agora que já estamos mais familiarizados com fatoriais, é hora de introduzir o conceito de permutação simples. Lembra-se do tipo de problema citado no início do texto? Pois é, problemas assim são conhecidos como problemas de permutação simples. Em problemas de combinatória, costuma-se indicar por permutações simples as maneiras de se organizar n objetos distintos (pessoas, malas, livros, etc.) em uma fila. O número total desse tipo de organização para n objetos distintos é denotado, geralmente, por P_n.
Podemos utilizar o PFC e resolver o problema geral de uma permutação simples com n objetos distintos: calcular a quantidade de maneiras de dispormos n diferentes objetos em fila. Para tanto, vamos realizar um raciocínio semelhante ao realizado no início do texto: calcular o número de maneiras que podemos escolher o objeto que ocupará o primeiro lugar da fila, depois o segundo lugar, depois o terceiro, até esgotar as [tex]n[/tex] posições da fila.

n escolhas		(n-1) escolhas		…		2 escolhas		1 escolha
1º lugar da fila		2º lugar da fila				(n-1)º lugar da fila		nº lugar da fila

A resposta será [tex]n![/tex] , não será?

Portanto, o número de permutações simples de [tex]n[/tex] objetos em fila fica definido pela igualdade [tex] P_n=n![/tex].

Útil e fácil!
Formalmente:

Permutações simples são definidas como maneiras de organizarmos [tex]n[/tex] objetos distintos em uma fila. O número total de permutações simples é denotado por [tex]P_n[/tex] e é verificada a igualdade [tex]P_n=n![/tex]

Pequenas atividades:
1. Quantos algarismos você acha que o número 14! possui?
2. Em quantas ordens diferentes você pode pedir o autógrafo dos 11 jogadores titulares de um time de futebol?
A maquineta disponibilizada abaixo poderá ajudar nos cálculos da segunda atividade e também na hora de conferir o palpite da primeira. Além disso, você poderá utilizá-la para calcular o fatorial de qualquer número natural menor que 21.

É importante lembrar de que o conceito de permutação simples é constantemente ligado ao de fatorial, mas a recíproca nem sempre é verdadeira! Há outras áreas da matemática que utilizam o fatorial; não somente a Contagem e a Combinatória.

---

---

---

---