Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 3ª série do E. M.- Nível de dificuldade: Médio)
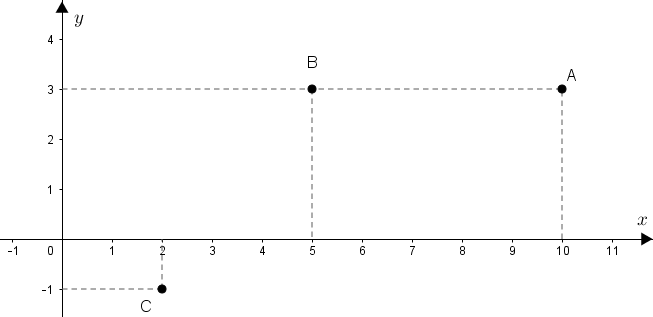
Determinar a área do losango ABCD sabendo que as coordenadas dos vértices A, B e C em um mesmo plano cartesiano xOy são dadas por:
- A=(10,3) ; B=(5,3) e C=(2,-1).
AJUDA
 |
Para resolver este problema vamos utilizar noções básicas de plano cartesiano.
Talvez o vídeo abaixo possa ajudar! |
Referencial Cartesiano (Abcissas e ordenadas)
Lembretes e notações
Em um plano cartesiano [tex]xOy[/tex], considere os pontos [tex]A=\left(x_A,y_A\right)\,[/tex] e [tex]\,B=\left(x_B,y_B\right)\,.[/tex]
(1) A distância entre os pontos [tex]A\,[/tex] e [tex]\,B[/tex], denotada por [tex]d_{AB}[/tex], é definida por:
[tex]\qquad d_{AB}=\sqrt{\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2\,}[/tex].
(2) O ponto médio dos pontos [tex]A\,[/tex] e [tex]\,B[/tex], denotado por [tex]M_{AB}[/tex], é o ponto definido por:
[tex]\qquad M_{AB}=\left(\dfrac{x_A+x_B}{2}\,,\, \dfrac{y_A+y_B}{2}\right)[/tex].
(3) Um losango possui os quatro lados congruentes.
(4) Em todo losango, as diagonais intersectam-se perpendicularmente nos respectivos pontos médios.
✐ Denotaremos o segmento de reta definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e seu respectivo comprimento por [tex]XY[/tex].
Solução
A partir dos Lembretes (3) e (4), podemos decompor um losango em quatro triângulos retângulos congruentes ou em dois triângulos, não necessariamente retângulos, congruentes, conforme ilustram as duas imagens a seguir.
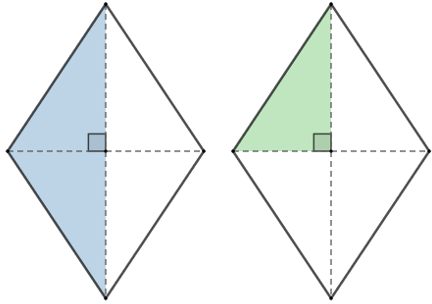
Dessa forma, sequer precisamos do quarto vértice do paralelogramo do problema para calcular a sua área. Assim, vamos inicialmente fixar um plano cartesiano [tex]xOy[/tex] e representar os pontos [tex]A,B\,[/tex] e [tex]\, C\,[/tex] para melhor visualizarmos a solução.
I – Vamos determinar o ponto médio comum das duas diagonais do losango utilizando os vértices [tex]A\,[/tex] e [tex]\,C[/tex], para podermos calcular a altura do triângulo [tex]ABC[/tex]. A área do losango será, então, duas vezes a área desse triângulo.
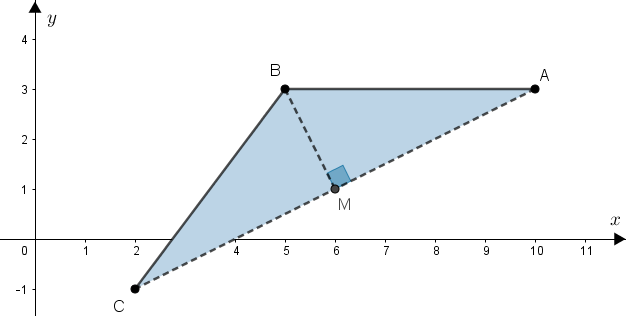
- Ponto médio da diagonal [tex]\overline{AC}[/tex]:
[tex]\qquad M_{AC}=\left(\dfrac{x_A+x_C}{2}\,,\, \dfrac{y_A+y_C}{2}\right)\\
\qquad M_{AC}=\left(\dfrac{10+2}{2}\,,\, \dfrac{3-1}{2}\right)\\
\qquad M_{AC}=\left(6\,,\,1\right).
[/tex]
Vamos agora determinar os comprimentos dos segmentos [tex]\overline{AC}\,[/tex] e [tex]\,\overline{BM}[/tex], respectivamente, base e altura do triângulo [tex]ABC\,.[/tex]
- Comprimento do segmento [tex]\overline{AC}\,[/tex]:
- Comprimento do segmento [tex]\overline{BM}\,[/tex]:
- Área do triângulo [tex]ABC[/tex]:
[tex]\qquad d_{AC}=\sqrt{\left(x_A-x_C\right)^2+\left(y_A-y_C\right)^2\,}\\
\qquad d_{AC}=\sqrt{\left(10-2\right)^2+\left(3-(-1)\right)^2\,}\\
\qquad d_{AC}=\sqrt{8^2+4^2\,}=\sqrt{64+16\,}\\
\qquad d_{AC}=\sqrt{80\,}.[/tex]
[tex]\qquad d_{BM}=\sqrt{\left(x_B-x_M\right)^2+\left(y_B-y_M\right)^2\,}\\
\qquad d_{BM}=\sqrt{\left(5-6\right)^2+\left(3-1\right)^2\,}\\
\qquad d_{BM}=\sqrt{(-1)^2+2^2\,}=\sqrt{1+4\,}\\
\qquad d_{BM}=\sqrt{5\,}.[/tex]
[tex]\qquad \textcolor{#0099CC}{S_{ABC}=\dfrac{base \times altura}{2}}\\
\qquad \textcolor{#0099CC}{S_{ABC}=\dfrac{\sqrt{80\,}\times \sqrt{5\,}}{2}}\\
\qquad \textcolor{#0099CC}{S_{ABC}=\dfrac{\sqrt{400\,}}{2}}\\
\qquad \textcolor{#0099CC}{S_{ABC}=10}.\\
[/tex]
Portanto, a área do losango [tex]ABCD[/tex] é [tex]\fcolorbox{black}{#d5e4ef}{$2 \times 10=20$}[/tex] unidades de área.
II – Vamos utilizar o ponto médio comum das duas diagonais do losango já calculado, [tex]M_{AC}=\left(6\,,\,1\right)[/tex], para calcularmos a medida do cateto [tex]\overline{MA}\,[/tex] do triângulo retângulo [tex]BMA\, .[/tex] A medida de [tex]\, \overline{MB}[/tex] já está calculada: [tex] d_{BM}=\sqrt{5\,}\,.[/tex] A área do losango será, dessa vez, quatro vezes a área desse triângulo.
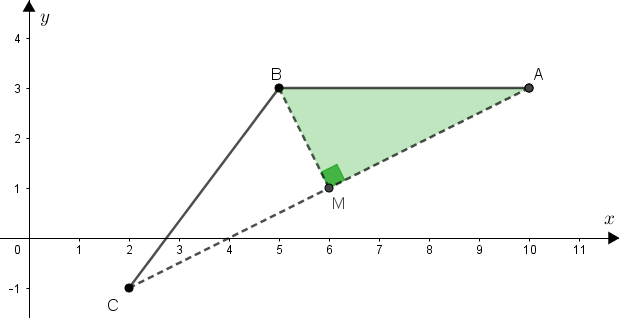
- Comprimento do segmento [tex]\overline{MA}\,[/tex]:
- Área do triângulo [tex]BMA[/tex]:
[tex]\qquad d_{MA}=\sqrt{\left(x_M-x_A\right)^2+\left(y_M-y_A\right)^2\,}\\
\qquad d_{MA}=\sqrt{\left(6-10\right)^2+\left(1-3\right)^2\,}\\
\qquad d_{MA}=\sqrt{(-4)^2+(-2)^2\,}=\sqrt{16+4\,}\\
\qquad d_{MA}=\sqrt{20\,}.[/tex]
[tex]\qquad \textcolor{#009900}{S_{BMA}=\dfrac{base \times altura}{2}}\\
\qquad \textcolor{#009900}{S_{BMA}=\dfrac{\sqrt{20\,}\times \sqrt{5\,}}{2}}\\
\qquad \textcolor{#009900}{S_{BMA}=\dfrac{\sqrt{100\,}}{2}}\\
\qquad \textcolor{#009900}{S_{BMA}=5}.\\
[/tex]
Portanto, a área do losango [tex]ABCD[/tex] é [tex]\fcolorbox{black}{#bfb}{$4 \times 5=20$}[/tex] unidades de área.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
