Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F.- Nível de dificuldade: Médio)
Após assistir a um filme sobre as aventuras do “Rei Arthur e os Cavaleiros da Távola Redonda”, o pequeno Artur resolveu fazer flechas e espadas para brincar. Ele rapidamente percebeu que poderia fazer belas pontas para suas flechas a partir de folhas de papel em formato de quadrados com [tex]1 \text{ dm}[/tex] de lado. Para isso, bastava cortar um quadrado num dos cantos de cada folha e, no pedaço do papel em forma de L restante, pintar uma parte como mostra a figura.
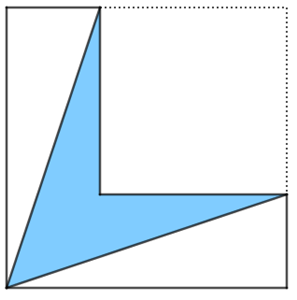
Depois de ter construído várias pontas, Artur reparou que a medida da área da região pintada em cada folha era exatamente um terço da medida da área do respectivo L.
Qual o comprimento do lado do quadrado que o Artur cortou em cada folha de papel que utilizou?
Adaptado da XIV ONM, 2012.
Solução
Vamos denotar por [tex]x[/tex] o comprimento em decímetros do lado do quadrado que o Artur cortou em cada folha de papel que utilizou. Observe que, para que o L seja definido, devemos ter [tex]0 \lt x \lt 1 \,.[/tex]
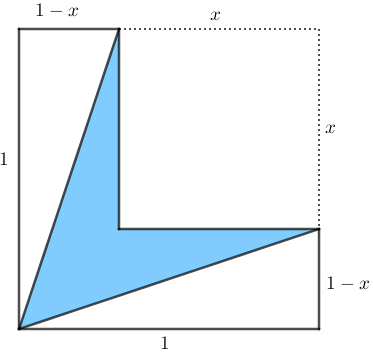
Perceba que ficam perfeitamente determinadas as medidas das áreas não pintadas do L, já que estas são triângulos retângulos de catetos com comprimentos [tex]1 \text{ dm}[/tex] e [tex](1-x) \text{ dm}[/tex]; cada uma dessas áreas mede [tex]\boxed{A_b=\dfrac{1 \cdot (1-x)}{2}=\dfrac{1-x}{2} \text{ dm}^2}\,.[/tex]
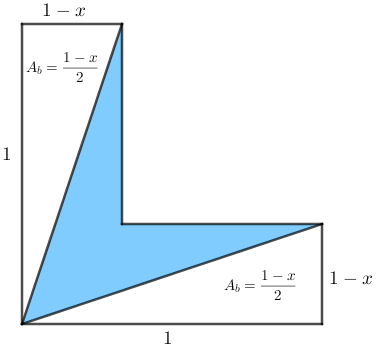
Segundo informações dadas no problema, a medida da área da região pintada em cada folha era exatamente um terço da medida da área do L; assim, a área branca total corresponde a [tex]2/3[/tex] da área do L, ou seja, [tex]\boxed{2\cdot A_b=\dfrac{2}{3} \cdot A_L}[/tex].
Como a área do L é [tex]\boxed{A_L=1^2-x^2=(1-x^2) \text{ dm}^2}[/tex], segue que:
[tex]\qquad 2\cdot A_b=\dfrac{2}{3} \cdot A_L\\
\qquad 2\cdot \dfrac{1-x}{2}=\dfrac{2}{3}\cdot (1-x^2) \\
\qquad \cancel{2}\cdot \dfrac{1-x}{\cancel{2}}=\dfrac{2}{3}\cdot (1-x^2) \\
\qquad 3\cdot (1-x)=2\cdot (1-x^2) \\
\qquad 3\cdot \cancel{(1-x)}\stackrel{x\ne 1}{=}2\cdot \cancel{(1-x)} \cdot (1+x)\\
\qquad 3=2+2x\\
\qquad x=\dfrac{1}{2}\,.[/tex]
Portanto, o comprimento do lado do quadrado que o Artur cortou em cada folha de papel que utilizou era de [tex]\,\fcolorbox{black}{#eee0e5}{$0,5 \text{ dm}$}\,[/tex], ou seja, [tex]\,\fcolorbox{black}{#eee0e5}{$5 \text{ cm}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
