Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 2º ano do E. M.- Nível de dificuldade: Médio)
Três das seis faces de um paralelepípedo retorretângulo têm as seguintes áreas: [tex] 192\,\text{cm}^2[/tex], [tex]336\,\text{cm}^2[/tex] e [tex]252\,\text{cm}^2 [/tex].
Qual a distância entre dois vértices desse paralelepípedo que não estejam na mesma face?
Extraído da IV ONEM, 2007.

Lembrete
Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
Solução
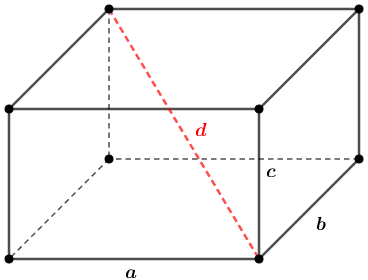
Vamos supor que os comprimentos dos lados do paralelepípedo retorretângulo do problema sejam [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] centímetros, conforme indica a figura a seguir.
Como o problema pede a distância entre dois vértices que não estejam na mesma face desse paralelepípedo, precisamos calcular o comprimento [tex]\textcolor{red}{d}[/tex] de uma de suas diagonais; por exemplo, a diagonal colorida de vermelho na mesma figura.
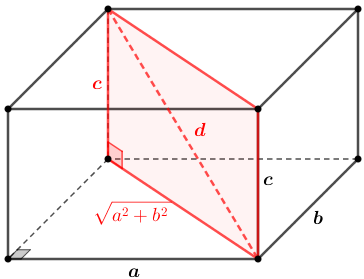
Observando a próxima figura, vemos que o comprimento [tex]\textcolor{red}{d}[/tex] é dado por [tex]\fcolorbox{red}{#ffffff}{$\textcolor{red}{d=\sqrt{a^2+b^2+c^2}}$}\,[/tex], consequência de duas aplicações do Teorema de Pitágoras.
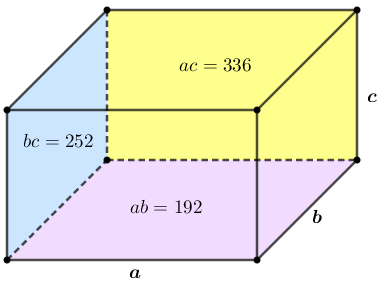
Como [tex]a[/tex], [tex]\,b\,[/tex] e [tex]\,c\,[/tex] são medidas genéricas, podemos supor, sem perda de generalidade, que:
- a face determinada pelos lados de comprimentos [tex]a[/tex] e [tex]b[/tex] centímetros tem área igual a [tex]192\,\text{cm}^2[/tex];
- a face determinada pelos lados de comprimentos [tex]a[/tex] e [tex]c[/tex] centímetros tem área igual a [tex]336\,\text{cm}^2[/tex];
- a face determinada pelos lados de comprimentos [tex]b[/tex] e [tex]c[/tex] centímetros tem área igual a [tex]252\,\text{cm}^2[/tex];
e, assim, [tex]ab=192[/tex], [tex]ac=336[/tex] e [tex]bc=252\,.[/tex]
Observe que
[tex]\qquad \left(abc\right)^2=\left(ab\right)\left(ac\right)\left(bc\right)[/tex]
[tex]\qquad \left(abc\right)^2=192 \times 336 \times 252[/tex]
e
[tex]\qquad \begin{align*}\dfrac{\left(abc\right)^2}{\left(bc\right)^2}+\dfrac{\left(abc\right)^2}{\left(ac\right)^2}+\dfrac{\left(abc\right)^2}{\left(ab\right)^2}
&=\dfrac{a^2\cdot\left(bc\right)^2}{\left(bc\right)^2}+\dfrac{b^2\cdot\left(ac\right)^2}{\left(ac\right)^2}+\dfrac{c^2\cdot \left(ab\right)^2}{\left(ab\right)^2}\\
&=\dfrac{a^2\cdot \color{blue}{\cancel{\left(bc\right)^2}}}{\color{blue}{\cancel{\left(bc\right)^2}}}+\dfrac{b^2\cdot\color{red}{\cancel{\left(ac\right)^2}}}{\color{red}{\cancel{\left(ac\right)^2}}}+\dfrac{c^2\cdot \color{#FF00FF}{\cancel{\left(ab\right)^2}}}{\color{#FF00FF}{\cancel{\left(ab\right)^2}}}\\
&=a^2+b^2+c^2\; ;
\end{align*}[/tex]
assim, segue que:
[tex]\qquad a^2+b^2+c^2=\dfrac{\left(abc\right)^2}{\left(bc\right)^2}+\dfrac{\left(abc\right)^2}{\left(ac\right)^2}+\dfrac{\left(abc\right)^2}{\left(ab\right)^2}\,\\
\qquad a^2+b^2+c^2=\dfrac{192 \times 336 \times 252}{252^2}+\dfrac{192 \times 336 \times 252}{336^2}+\dfrac{192 \times 336 \times 252}{192^2}\\
\qquad a^2+b^2+c^2=\dfrac{192 \times 336}{252}+\dfrac{192 \times 252}{336}+\dfrac{336 \times 252}{192}\\
\qquad a^2+b^2+c^2=256+144+441\\
\qquad a^2+b^2+c^2=841\,.[/tex]
Portanto:
[tex]\qquad \textcolor{red}{d=\sqrt{a^2+b^2+c^2}}\\
\qquad\textcolor{red}{d=\sqrt{841}}\\
\qquad \textcolor{red}{d=29}.[/tex]
Logo, a distância entre dois vértices que não estão na mesma face do paralelepípedo retorretângulo definido no problema é [tex]\, \fcolorbox{black}{#eee0e5}{$29 \text{ cm}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
