Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Fácil)
A Figura 1 mostra um triângulo retângulo [tex]ABC[/tex] e um retângulo [tex]BDEF[/tex], sendo [tex]C[/tex] um ponto do segmento [tex]BF.[/tex] As medidas que aparecem na figura estão expressas em centímetros.
Ao girarmos a Figura 1 em torno do segmento [tex]AD[/tex], girando [tex]360^\circ[/tex], obtemos o sólido que aparece na Figura 2.
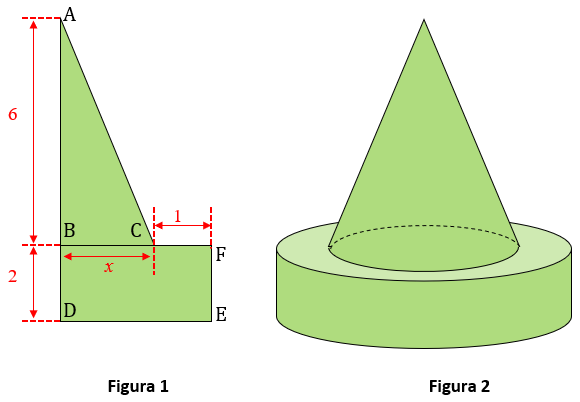
Considerando o cone e o cilindro que compõem o sólido mostrado na Figura 2, pergunta-se:
(a) Para que valores de [tex]x[/tex] o volume do cone será menor que o volume do cilindro?
(b) O que podemos concluir a partir da resposta do item anterior?
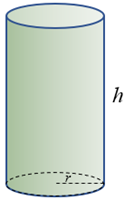
Lembretes
✐ Volume de um cilindro circular reto cujo comprimento da altura é [tex]h[/tex] e o comprimento do raio da base é [tex]r[/tex]:
[tex]\qquad \qquad \boxed{Volume=\pi\,r^2 h}.[/tex]
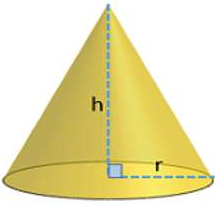
✐ Volume de um cone circular reto cujo comprimento da altura é [tex]h[/tex] e o comprimento do raio da base é [tex]r[/tex]:
[tex]\qquad \qquad \boxed{Volume= \dfrac{\pi r^2h}{3}}. [/tex]
Solução
Observemos separadamente o cilindro e o cone que compõem o sólido de revolução ilustrado na Figura 2.
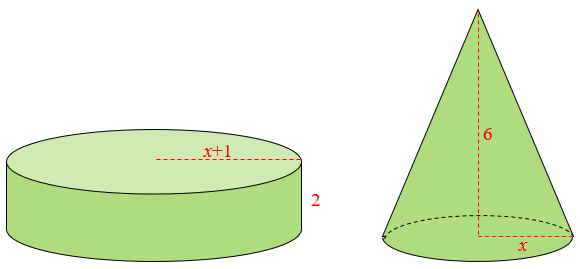
De acordo com as fórmulas indicadas nos Lembretes, podemos calcular os volumes [tex]V_{c\, i}[/tex] do cilindro e [tex]V_{c\, o}[/tex] do cone como se segue:
| [tex]\qquad \qquad V_{c\, i}=\pi\, r^2 h[/tex] [tex]\qquad \qquad V_{c\, i}=\pi\cdot (x+1)^2 \cdot 2\\ \qquad \qquad V_{c\, i}=2\pi\cdot \left(x^2+2x+1\right)\\ \qquad \qquad V_{c\, i}=2\pi x^2+4\pi x+2\pi[/tex] |
[tex]\qquad \quad V_{c\, o}=\dfrac{\pi r^2h}{3}\\ \qquad \quad V_{c\, o}=\dfrac{\pi \cdot x^2 \cdot 6}{3}\\ \qquad \quad V_{c\, o}=\pi \cdot x^2 \cdot 2\\ \qquad \quad V_{c\, o}=2\pi x^2 [/tex] |
(a) Para determinarmos para quais valores de [tex]x[/tex] o volume do cone será menor que o volume do cilindro, vamos impor a condição [tex]V_{c\, o} \lt V_{c\, i}[/tex]. Vejamos:
[tex]\qquad V_{c\, o} \lt V_{c\, i}\\
\qquad \cancel{2\pi x^2} \lt \cancel{2\pi x^2}+4\pi x+2\pi\\
\qquad 0 \lt 4\pi x+2\pi\\
\qquad -2\cancel{\pi} \lt 4\cancel{\pi}x\\
\qquad \dfrac{-2}{4} \lt x\\
\qquad x \gt \dfrac{-1}{2}.[/tex]
Mas observe que [tex]x[/tex] denota uma medida de comprimento, logo representa um valor positivo. Assim, o volume do cone será menor que o volume do cilindro para todos os valores reais de [tex]x[/tex] tais que [tex]\, \fcolorbox{black}{#eee0e5}{$x \gt\, 0$}\, .[/tex]
(b) Como no contexto do problema [tex]x[/tex] é uma medida de comprimento, e portanto sempre positiva, para os sólidos definidos no problema o volume do cone será SEMPRE menor que o volume do cilindro.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
