Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Muito Difícil)
(XXIX Olimpíada Madri, 1993 – Adaptado) Matheus ganhou um jogo eletrônico em cuja tela aparece um esquema como o mostrado na figura abaixo.
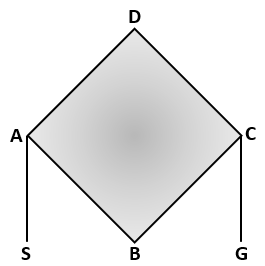
Nesse jogo, cada partida é jogada da seguinte forma:
(1) No início da partida, uma bola aparece no ponto S.
(2) Cada vez que o jogador toca na tela, essa bola se move até a extremidade oposta de um dos segmentos com extremidade no ponto onde a bola se encontra. Por exemplo, se a bola está sobre o ponto D, ela poderá se mover apenas para o ponto A ou para o ponto C; mas se a bola estiver sobre o ponto C, outro exemplo, ela poderá se movimentar até B ou D ou G.
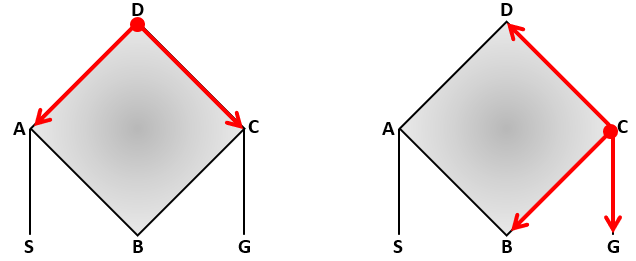
(3) A partida termina quando ocorrer o primeiro de um destes dois casos:
- A bola volta para o ponto S, e neste caso o jogador perde a partida.
- A bola chega no ponto G, e então o jogador ganha a partida.
Se a chance de, estando em um ponto, a bola se mover para qualquer dos pontos possíveis é a mesma, qual probabilidade é maior: a de o jogador ganhar ou a de ele perder?

AJUDA
✐ Dada uma progressão geométrica infinita [tex](a_1,a_1\cdot q, a_1\cdot q^2,\cdots,a_1\cdot q^{n-1},\cdots)[/tex] de razão [tex]q\, [/tex], [tex]0\lt q\lt 1[/tex], o limite da soma de todos os seus termos pode ser calculado pela fórmula
\begin{equation}S=\dfrac{a_{1}}{1-q}\, .\end{equation}
✐ Sabemos que um evento [tex]E[/tex] pode ocorrer ou não. Se o evento [tex]E[/tex] for relativo a um espaço amostral [tex]\, \Omega[/tex], o evento associado à não ocorrência de [tex]E[/tex] é denominado o complementar de [tex]E[/tex] com relação a [tex]\, \Omega[/tex] e é denotado por [tex]\overline{E}[/tex].
- Logo, [tex]\overline{E}[/tex] ocorre se, e somente se, [tex]E[/tex] não ocorrer.
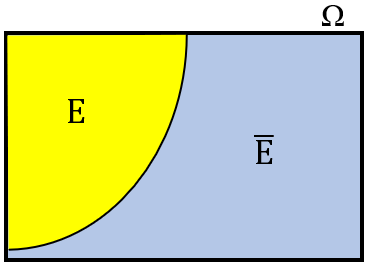
Dessa forma, se [tex]P[/tex] for a probabilidade de que o evento [tex]E[/tex] ocorra (sucesso) e [tex]Q[/tex] for a probabilidade de que [tex]E[/tex] não ocorra (insucesso), então [tex]Q[/tex] é a probabilidade do evento complementar [tex]\overline{E}[/tex], ou simplesmente probabilidade complementar de [tex]P[/tex], e temos a seguinte relação: [tex]\boxed{P+Q=1}\, .[/tex]
Solução
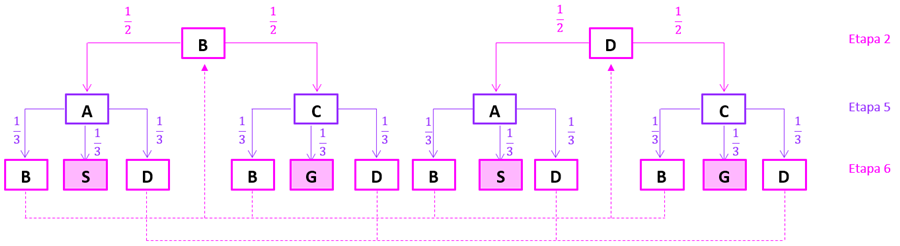
Podemos representar as quatro primeiras etapas possíveis para o jogo utilizando o diagrama de árvore abaixo.
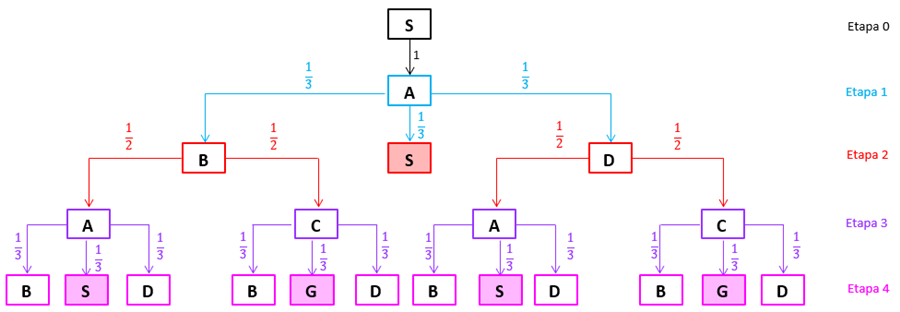
-
[tex]\textcolor{#800000}{(i)}[/tex] Vamos, inicialmente, determinar a possibilidade de o jogador ganhar uma partida do jogo.
- Observe pelo diagrama que o jogador não consegue ganhar na primeira, nem na segunda e nem na terceira etapa.
- A primeira chance para o jogador ganhar é na quarta etapa e existem dois caminhos independentes:
[tex]S \rightarrow \textcolor{#3BB9FF}{A} \rightarrow \textcolor{red}{B} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{G}\qquad \boxed{\text{ou}}\qquad S \rightarrow \textcolor{#3BB9FF}{A} \rightarrow \textcolor{red}{D} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{G} \, .[/tex]
A probabilidade de isso acontecer é:
[tex]\qquad P_4=\left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\right) \boxed{+} \left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\right)\\
\qquad P_4=2 \times \left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\right) \\
\qquad \boxed{P_4=\dfrac{1}{3^2}}.[/tex] - A próxima chance de o jogador vencer é na sexta etapa. Para que isso ocorra, temos oito caminhos diferentes:
- A terceira chance de o jogador vencer é na oitava etapa. Para que isso ocorra, temos trinta e dois caminhos distintos. Esses caminhos podem ser visualizados no quadro abaixo.
- Observe que o jogador só pode vencer em etapas pares, a partir da terceira e, de maneira geral, a probabilidade de o jogador vencer na Etapa [tex]2n[/tex], [tex]n[/tex] um número natural maior do que [tex]1[/tex], é dada por:
- Observe no diagrama inicial que o jogador não consegue perder na primeira etapa.
- A primeira possibilidade de o jogador perder é na segunda etapa e para isso existe apenas um caminho:
[tex]S \rightarrow \textcolor{#3BB9FF}{A} \rightarrow \textcolor{red}{S} .[/tex]
A probabilidade de isso acontecer é:
[tex]\qquad P_2=1 \times \dfrac{1}{3} = \dfrac{1}{3}[/tex] - A próxima chance de o jogador perder é na quarta etapa. Para que isso ocorra, temos dois caminhos diferentes:
[tex]S \rightarrow \textcolor{#3BB9FF}{A} \rightarrow \textcolor{red}{B} \rightarrow \textcolor{#893BFF}{A} \rightarrow \textcolor{#FF00FF}{S}\qquad \boxed{\text{ou}}\qquad S \rightarrow \textcolor{#3BB9FF}{A} \rightarrow \textcolor{red}{D} \rightarrow \textcolor{#893BFF}{A} \rightarrow \textcolor{#FF00FF}{S} .[/tex]
A probabilidade de isso acontecer é:
[tex]\qquad P_4=\left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\right) \boxed{+} \left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\right)\\
\qquad P_4=2 \times \left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\right) \\
\qquad \boxed{P_4=\dfrac{1}{3^2}}.[/tex] - As próximas etapas nas quais o jogador poderá perder são as Etapas 6, 8, 10, etc. e os cálculos das probabilidades de perda são exatamente iguais aos cálculos das probabilidades de o jogador ganhar nas respectivas etapas.
[tex]S \rightarrow \textcolor{#3BB9FF}{A} \rightarrow \textcolor{red}{B} \rightarrow \textcolor{#893BFF}{A} \rightarrow \textcolor{#FF00FF}{B} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{G}\quad \boxed{\text{ou}}\quad S \rightarrow \textcolor{#3BB9FF}{A} \rightarrow \textcolor{red}{B} \rightarrow \textcolor{#893BFF}{A} \rightarrow \textcolor{#FF00FF}{D} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{G}\quad \boxed{\text{ou}}\\
S \rightarrow \textcolor{#3BB9FF}{A} \rightarrow \textcolor{red}{B} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{B} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{G}\quad \boxed{\text{ou}} \quad S \rightarrow \textcolor{#3BB9FF}{A} \rightarrow \textcolor{red}{B} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{D} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{G}\quad \boxed{\text{ou}}\\
S \rightarrow \textcolor{#3BB9FF}{A} \rightarrow \textcolor{red}{D} \rightarrow \textcolor{#893BFF}{A} \rightarrow \textcolor{#FF00FF}{B} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{G}\quad \boxed{\text{ou}}\quad S \rightarrow \textcolor{#3BB9FF}{A} \rightarrow \textcolor{red}{D} \rightarrow \textcolor{#893BFF}{A} \rightarrow \textcolor{#FF00FF}{D} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{G}\quad \boxed{\text{ou}}\\
S \rightarrow \textcolor{#3BB9FF}{A} \rightarrow \textcolor{red}{D} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{B} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{G}\quad \boxed{\text{ou}}\quad S \rightarrow \textcolor{#3BB9FF}{A} \rightarrow \textcolor{red}{D} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{D} \rightarrow \textcolor{#893BFF}{C} \rightarrow \textcolor{#FF00FF}{G}\,.[/tex]
- Esses caminhos equivalem a, ao chegar na Etapa 4, voltar para a Etapa 2, refazer a Etapa 3 como Etapa 5 e refazer a Etapa 4 como Etapa 6.
Vamos então calcular a probabilidade de se ganhar a partida na sexta etapa:
[tex]\;\begin{align*}P_6=&\left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\times \dfrac{1}{2} \times \dfrac{1}{3}\right) \boxed{+} \left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\times \dfrac{1}{2} \times \dfrac{1}{3}\right)\boxed{+}\\
&\left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\times \dfrac{1}{2} \times \dfrac{1}{3}\right) \boxed{+} \left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\times \dfrac{1}{2} \times \dfrac{1}{3}\right) \boxed{+}\\
&\left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\times \dfrac{1}{2} \times \dfrac{1}{3}\right)\boxed{+} \left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\times \dfrac{1}{2} \times \dfrac{1}{3}\right) \boxed{+}\\
&\left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\times \dfrac{1}{2} \times \dfrac{1}{3}\right) \boxed{+} \left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\times \dfrac{1}{2} \times \dfrac{1}{3}\right)\end{align*}\\
\;P_6=8 \times \left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\right) \\
\;\boxed{P_6=\dfrac{2}{3^3}}.[/tex]

A probabilidade de cada um desses caminhos é a mesma; portanto, a probabilidade de o jogador ganhar na oitava etapa pode ser assim calculada:
[tex]\qquad \left.
\begin{array} {l}
P_8 &=\left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\times \dfrac{1}{2} \times \dfrac{1}{3}\times \dfrac{1}{2} \times \dfrac{1}{3}\right) \boxed{+}\\
&\qquad \qquad \vdots\\
& \boxed{+} \left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\times \dfrac{1}{2} \times \dfrac{1}{3} \times\dfrac{1}{2} \times \dfrac{1}{3}\right)\end{array} \right\}{32\, parcelas}[/tex]
[tex]\qquad P_8=32 \times \left(1 \times \dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{3}\times \dfrac{1}{2} \times \dfrac{1}{3}\times \dfrac{1}{2} \times \dfrac{1}{3}\right)\\
\qquad \boxed{P_8=\dfrac{2^2}{3^4}}.[/tex]
[tex] \qquad \boxed{P_{2n}=\dfrac{2^{n-2}}{3^n}}.[/tex]
Pelo até aqui exposto, temos que o jogador vencerá em uma Etapa par maior do que [tex]3[/tex], mas não sabemos exatamente em qual Etapa, ou seja, o jogador vencerá na Etapa 4 ou Etapa 6 ou Etapa 8 ou Etapa 10 ou …
Dessa forma, a probabilidade de o jogador vencer a partida é:
[tex] \qquad P_v=P_4 \textcolor{red}{+}P_6 \textcolor{red}{+}P_8 \textcolor{red}{+}P_{10} \textcolor{red}{+} \cdots \textcolor{red}{+}P_{2n} \textcolor{red}{+} \cdots\\
\qquad P_v=\dfrac{1}{3^2}+\dfrac{2}{3^3} +\dfrac{2^2}{3^4} +\dfrac{2^3}{3^5} + \cdots +\dfrac{2^{n-2}}{3^n} + \cdots\, .[/tex]
Para calcular a soma [tex]P_v[/tex] de infinitas parcelas, observe que [tex]\left(\dfrac{1}{3^2},\dfrac{2}{3^3},\dfrac{2^2}{3^4} ,\dfrac{2^3}{3^5} ,\cdots ,\dfrac{2^{n-2}}{3^n} ,\cdots \quad \right) [/tex] é uma progressão geométrica infinita de razão [tex]q=\dfrac{2}{3}[/tex] . Portanto, utilizando a fórmula do lembrete, temos que:
[tex]\\
\qquad P_v=\dfrac{1}{3^2}+\dfrac{2}{3^3} +\dfrac{2^2}{3^4} +\dfrac{2^3}{3^5} + \cdots +\dfrac{2^{n-2}}{3^n} + \cdots\\
\qquad P_v=\dfrac{\frac{1}{3^2}}{1-\frac{2}{3}}=\dfrac{\frac{1}{9}}{\frac{1}{3}}\\
\qquad P_v=\dfrac{1}{9}\times \dfrac{3}{1}\\
\qquad \fcolorbox{black}{#eee0e5}{$P_v=\dfrac{1}{3}$} .\\[/tex]
[tex]\textcolor{#800000}{(ii)}[/tex] Vamos agora analisar a probabilidade de o jogador perder uma partida no jogo.
Perceba que a contagem das possibilidades de o jogador perder é igual a de ele ganhar, a menos de um detalhe: o jogador pode perder na Etapa 2.
Vejamos:
Aqui também sabemos que o jogador poderá perder na Etapa 2 ou na Etapa 4 ou na Etapa 6 ou na Etapa 8 ou na Etapa 10 ou … Mas não sabemos exatamente em qual Etapa.
Dessa forma, a probabilidade de o jogador perder a partida é:
[tex] \qquad P_p=P_2 \textcolor{red}{+}P_4 \textcolor{red}{+}P_6 \textcolor{red}{+}P_8 \textcolor{red}{+}P_{10} \textcolor{red}{+} \cdots \textcolor{red}{+}P_{2n} \textcolor{red}{+} \cdots\\
\qquad P_p=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{2}{3^3} +\dfrac{2^2}{3^4} +\dfrac{2^3}{3^5} + \cdots +\dfrac{2^{n-2}}{3^n} + \cdots\, .[/tex]
Como já calculamos a soma
[tex]\qquad \qquad \dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{2}{3^3} +\dfrac{2^2}{3^4} +\dfrac{2^3}{3^5} + \cdots +\dfrac{2^{n-2}}{3^n} + \cdots=\dfrac{1}{3}[/tex],
segue que
[tex]\, \,
\qquad P_p=\dfrac{1}{3}+\left(\dfrac{1}{3^2}+\dfrac{2}{3^3} +\dfrac{2^2}{3^4} +\dfrac{2^3}{3^5} + \cdots +\dfrac{2^{n-2}}{3^n} + \cdots\right)\\
\qquad P_p=\dfrac{1}{3}+\dfrac{1}{3}\\
\qquad P_p=\dfrac{2}{3}\, .\\[/tex]
Poderíamos ter poupado esses cálculos se tivéssemos utilizado a “probabilidade complementar” apresentada na AJUDA.
Nesse caso, o evento [tex]E[/tex] é "o jogador ganhar uma partida" e o evento [tex]\overline{E}[/tex] é "o jogador perder a partida".
Assim, como os eventos são independentes, segue que:
[tex]\qquad \qquad \fcolorbox{black}{#eee0e5}{$P_p$}=Q=1-P=1-P_v=1-\dfrac{1}{3}=\fcolorbox{black}{#eee0e5}{$\dfrac{2}{3}$}\,.[/tex]
Observação: Perceba que a probabilidade de [tex]\, \fcolorbox{black}{#eee0e5}{$\dfrac{1}{3}$}[/tex] de o jogador vencer a partida e de [tex]\, \fcolorbox{black}{#eee0e5}{$\dfrac{2}{3}$}[/tex] de ele perder são resultados teóricos. Nenhuma partida terá duração infinita, já que nenhum jogador viverá eternamente para jogar infinitas vezes.
Os resultados práticos seriam:
► quanto mais etapas o jogador jogar, mais a probabilidade de ele ganhar se aproxima de [tex]\dfrac{1}{3}[/tex];
► quanto mais etapas o jogador jogar, mais a probabilidade de ele perder se aproxima de [tex]\dfrac{2}{3}[/tex].
A tabela abaixo ilustra essas duas afirmações.
| Probabilidade de o jogador ganhar | Probabilidade de o jogador perder | |
| Até a Etapa 2:[tex]\, \, \frac{1}{3}\approx 33,33\%[/tex] | ||
| Até a Etapa 4: [tex]\, \frac{1}{9}\approx 11,11\%[/tex] | Até a Etapa 4:[tex]\, \frac{4}{9}\approx 44,44\%[/tex] | |
| Até a Etapa 6: [tex]\, \frac{5}{27}\approx 18,52\%[/tex] | Até a Etapa 6:[tex]\, \frac{14}{27}\approx 51,85\%[/tex] | |
| Até a Etapa 8: [tex]\, \frac{19}{81}\approx 23,46\%[/tex] | Até a Etapa 8:[tex]\, \frac{46}{27}\approx 56,79\%[/tex] | |
| Até a Etapa 10: [tex]\, \frac{65}{243}\approx 26,75\%[/tex] | Até a Etapa 10:[tex]\, \frac{146}{243}\approx 60,08\%[/tex] | |
| Até a Etapa 12: [tex]\, \frac{211}{729}\approx 28,94\%[/tex] | Até a Etapa 12:[tex]\, \frac{454}{729}\approx 62,28\%[/tex] | |
| Até a Etapa 14: [tex]\, \frac{665}{2187}\approx 30,41\%[/tex] | Até a Etapa 14:[tex]\, \frac{1394}{2187}\approx 63,74\%[/tex] | |
| [tex]\vdots[/tex] | [tex]\vdots[/tex] | |
| [tex]\fcolorbox{black}{#eee0e5}{$\frac{1}{3}\approx 33,33\%$}[/tex] | [tex]\fcolorbox{black}{#eee0e5}{$\frac{2}{3}\approx 66,67\%$}[/tex] |
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
