(A) Problema para ajudar na escola: Vértices coloridos

Problema
(A partir do 7º ano do E. F. – Nível de dificuldade: Difícil)

(ONEM – 2008) Alguns dos dezesseis vértices do tabuleiro [tex]3 \times 3[/tex] mostrado na figura deverão ser coloridos e, em cada quadradinho do tabuleiro, está indicada a quantidade de vértices que devem ser coloridos no respectivo quadradinho.

• Por exemplo, o número [tex]2[/tex] que aparece no primeiro quadradinho da primeira linha indica que esse quadradinho deverá ter exatamente dois vértices coloridos.

No entanto, a pessoa encarregada de indicar os números nos nove quadradinhos se enganou e colocou uma letra no lugar do número do quadradinho central.

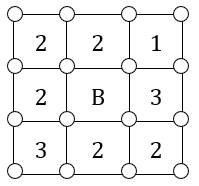
Quais as possibilidades de valores para [tex]B[/tex]?

Solução

Para a solução deste problema, denotaremos por [tex]Q_{n,m}[/tex] o quadradinho que está na linha [tex]n[/tex] e na coluna [tex]m[/tex] do tabuleiro.
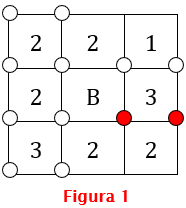
[tex]\textcolor{#800000}{(i)}[/tex] Vamos começar a nossa análise observando o quadradinho que está na segunda linha e na terceira coluna do tabuleiro, o qual denotaremos por [tex]Q_{2,3}[/tex].

• Vemos que três dos quatro vértices do quadradinho [tex]Q_{2,3}[/tex] devem ser pintados; logo, pelo menos um de seus vértices superiores e pelo menos um de seus vértices inferiores devem ser pintados. Mas devemos pintar apenas um dos vértices do quadradinho [tex]Q_{1,3}[/tex] acima dele; assim exatamente um de dois vértices superiores de [tex]Q_{2,3}[/tex] deve ser pintado e, consequentemente, devem ser pintados os seus dois vértices inferiores. Vamos colorir esses dois vértices inferiores na Figura 1, abaixo.
• Como apenas um dos vértices do quadradinho [tex]Q_{1,3}[/tex] deve ser pintado e já sabemos que um dos seus vértices inferiores vai ser pintado, os dois vértices superiores de [tex]Q_{1,3}[/tex] não serão pintados. Para lembrar desse fato, vamos retirar os dois pequenos círculos que demarcam esses vértices no tabuleiro mostrado na Figura 1. Não colorimos nenhum vértice superior de [tex]Q_{1,3}[/tex], pois não sabemos exatamente qual será colorido.
• Já sabemos que os dois vértices inferiores do quadradinho [tex]Q_{2,3}[/tex] serão pintados. Logo, como apenas dois dos vértices do quadrinho [tex]Q_{3,3}[/tex] serão pintados, necessariamente os dois vértices inferiores de [tex]Q_{3,3}[/tex] não serão pintados. Igualmente, vamos retirar os dois pequenos círculos que demarcam esses vértices no tabuleiro mostrado na Figura 1.

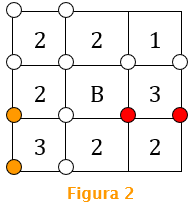
[tex]\textcolor{#800000}{(ii)}[/tex] Agora, vamos observar o quadradinho do canto inferior esquerdo do tabuleiro, o [tex]Q_{3,1}[/tex].

• Vemos que três dos vértices de [tex]Q_{3,1}[/tex] devem ser pintados, mas não podemos pintar os seus dois vértices à direita; pois, se assim o fizéssemos, o quadradinho [tex]Q_{3,2}[/tex] ficaria com três de seus vértices coloridos e isso não é possível, já que ele tem apenas dois vértices a serem pintados. Dessa forma os dois vértices esquerdos de [tex]Q_{3,1}[/tex] serão necessariamente pintados. Registraremos essa conclusão colorindo esses dois vértices na Figura 2. Não iremos colorir um dos vértices à esquerda de [tex]Q_{3,1}[/tex], pois não temos informação sobre qual será pintado.

[tex]\textcolor{#800000}{(iii)}[/tex] Finalmente, vamos tentar obter informações sobre o quadradinho central em questão, isto é, o quadradinho [tex]Q_{2,2}.[/tex]

• Já sabemos que pelo menos o vértice inferior direito de [tex]Q_{2,2}[/tex] vai ser colorido. No entanto não podemos colorir apenas esse vértice, pois, se assim fosse, teríamos problemas com o quadradinho [tex]Q_{1,2}[/tex]: como temos que pintar dois dos três vértices de [tex]Q_{1,2}[/tex] possíveis de serem pintados, necessariamente um dos vértices superiores de [tex]Q_{2,2}[/tex] vai ser pintado.

Logo, [tex]\boxed{B\ne 1}.[/tex]

• Tampouco podemos ter [tex]B=4[/tex]. pois, se isso ocorresse, teríamos três vértices de [tex]Q_{2,1}[/tex] pintados. E isso não poder ocorrer, já que a informação que temos é que [tex]Q_{2,1}[/tex] tem apenas dois de seus vértices coloridos.

Portanto, [tex]\boxed{B\ne 4}.[/tex]

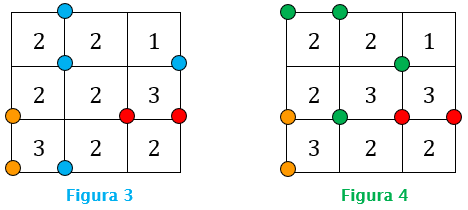
• Restam dois valores para [tex]B[/tex]: [tex]2[/tex] e [tex]3.[/tex] Para garantir que os dois valores são possíveis, mostraremos duas configurações para o tabuleiro que mostram que, de fato, [tex]B[/tex] pode assumir esses dois valores.
  Na Figura 3 consideramos [tex]B=2[/tex] e na Figura 4 consideramos [tex]B=3.[/tex]



Observe que poderíamos também ter feito a configuração mostrada na Figura 5 para [tex]B=2[/tex] e a configuração da Figura 6 para [tex]B=3.[/tex]

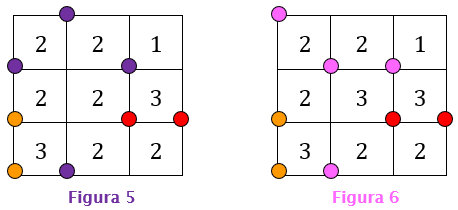
De qualquer forma, são duas as possibilidades de valores para [tex]B[/tex]: [tex]\boxed{B=2} [/tex] ou [tex] \boxed{B=3} .[/tex]

Solução elaborada pelos Moderadores do Blog.