Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
(XII Concurso de Primavera de Matemáticas, 2008 – Adaptado) Todos os hexágonos que aparecem na figura abaixo são regulares.
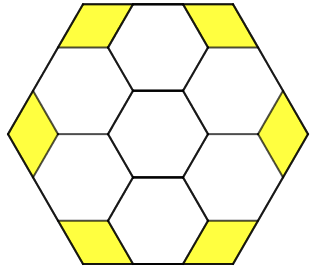
Se a área do hexágono maior mede [tex]810\,\text{cm}^2[/tex], quanto mede a área colorida de amarelo?

Lembretes
(1) A soma dos ângulos internos de um polígono convexo de [tex]n[/tex] lados [tex](n\gt 2)[/tex] é dada por:
[tex]\qquad \qquad \boxed{S_{i_n}=\left(n-2\right)\times 180^\circ}.[/tex]
(2) Todo quadrilátero convexo que tenha ângulos opostos com a mesma medida é um paralelogramo.
(3) A área [tex] A_{teq}[/tex] de um triângulo equilátero de lados com comprimento [tex]l[/tex] pode ser assim calculada:
[tex]\qquad A_{teq}=\dfrac{l^2\times \sqrt{3}}{4}.[/tex]
(4) A área [tex] A_{h}[/tex] de um hexágono regular de lados com comprimento [tex]l[/tex] pode ser assim calculada:
[tex]\qquad A_{h}=\dfrac{l^2\times 3\times \sqrt{3}}{2}.[/tex]
(5) Se um triângulo isósceles possui um ângulo de [tex]60^\circ[/tex], então esse triângulo é equilátero.
Solução 1
Observe que todos os hexágonos são convexos; assim, a soma das medidas dos ângulos internos de cada hexágono da figura pode ser assim calculada:
[tex]\qquad \qquad S_{i_6}=\left(6-2\right)\times 180^\circ= 720^\circ[/tex] .
Como os hexágonos da figura são regulares, seus ângulos internos têm a mesma medida:
[tex]\qquad \qquad \dfrac{720^\circ}{6}=120^\circ[/tex] .
Assim, cada quadrilátero amarelo tem dois ângulos opostos de [tex]60^\circ[/tex] (cada um é suplemento de um ângulo interno de um hexágono pequeno) e um terceiro ângulo que é ângulo do hexágono maior e portanto mede [tex]120^\circ[/tex] .
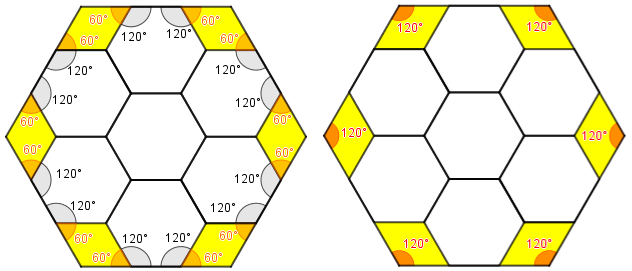
Dessa forma, como a soma das medidas dos ângulos internos de um quadrilátero é dada por
[tex]\qquad \qquad S_{i_4}=\left(4-2\right)\times 180^\circ= 360^\circ[/tex],
segue que a medida do quarto ângulo interno de cada quadrilátero amarelo é igual a
[tex]\qquad \qquad 360^\circ-2 \times 60^\circ-120^\circ=120^\circ[/tex] .
Com isso, concluímos que cada quadrilátero amarelo tem ângulos opostos com a mesma medida, o que nos garante que cada um é um paralelogramo. Mas como todos os hexágonos que aparecem na figura são regulares e o hexágono central tem lados em comum com os seis outros hexágonos pequenos, então todos os lados dos hexágonos pequenos têm o mesmo comprimento. Dessa forma,
- os quadriláteros amarelos são losangos com a mesma área.
Por outro lado, sabemos que a área do hexágono maior mede [tex]810\,\text{cm}^2[/tex]; assim, se [tex]L[/tex] é o comprimento em centímetros dos lados desse hexágono, segue do Lembrete 4 que:
[tex]\qquad 810=\dfrac{L^2\times 3\times \sqrt{3}}{2}[/tex]
[tex]\qquad L^2=\dfrac{540}{\sqrt{3}}.[/tex]
Como [tex]L \gt 0[/tex], segue ainda que:
[tex]\qquad L=\sqrt{\dfrac{540}{\sqrt{3}}}=\sqrt{\dfrac{36 \times 15}{\sqrt{3}}}=6\,\sqrt{\dfrac{15}{\sqrt{3}}}\,\text{cm}.[/tex]
Agora, se [tex]l[/tex] é o comprimento dos lados dos hexágonos pequenos, e consequentemente dos lados dos losangos amarelos, então:
[tex]\qquad L=3l\\
\qquad 6\,\sqrt{\dfrac{15}{\sqrt{3}}}=3l\\
\qquad l=2\,\sqrt{\dfrac{15}{\sqrt{3}}}\,\text{cm}.[/tex]
Perceba que para finalizar o problema precisamos calcular a área de um losango cujo lado mede [tex] l=2\,\sqrt{\dfrac{15}{\sqrt{3}}}\,\text{cm}[/tex] .
Para tanto, observe que a diagonal menor de cada losango amarelo divide-o, a princípio, em dois triângulos isósceles. Mas, como o ângulo oposto a essa diagonal mede [tex]60^\circ[/tex], esses triângulos, na verdade, são equiláteros, de acordo com o Lembrete 5 . Logo, utilizando o Lembrete 3 , podemos concluir que a área [tex]A_{la}[/tex] de cada losango amarelo é dada por:
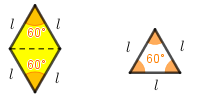
[tex]\qquad A_{la}=2 \times \dfrac{l^2\times \sqrt{3}}{4}\\
\qquad A_{la}=2 \times \dfrac{ \left(2\,\sqrt{\dfrac{15}{\sqrt{3}}}\right)^2\times \sqrt{3}}{4}\\
\qquad A_{la}=2 \times \dfrac{4 \times\dfrac{15}{\cancel{\sqrt{3}}}\times \cancel{\sqrt{3}}}{4} \\
\qquad A_{la}=2 \times \dfrac{\cancel{4} \times 15}{\cancel{4}}\\
\qquad A_{la}=2 \times 15\\
\qquad A_{la}=30\,\text{cm}^2 .[/tex]
Portanto, a área colorida de amarelo mede [tex]6 \times 30[/tex], ou seja, [tex]\fcolorbox{black}{#eee0e5}{$180\,\text{cm}^2$}[/tex].
Solução elaborada pelos Moderadores do Blog.
Solução 2
Poderíamos ter evitado os cálculos da solução anterior, se tivéssemos observado que cada hexágono pequeno da figura é regular e pode ser dividido em três losangos a partir de seus respectivos centros, como indicado na figura abaixo. Particularmente, cada um desses losangos tem a mesma área dos losangos amarelos da figura inicial.
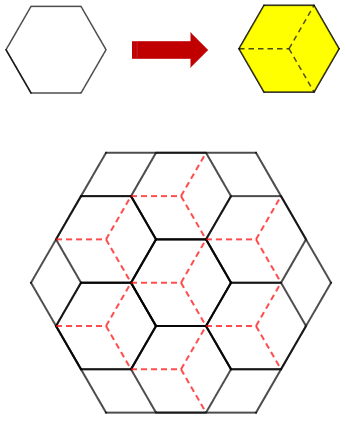
Com isso, o hexágono maior pode ser dividido em [tex]7 \times 3+6=27[/tex] losangos com áreas equivalentes às áreas dos losangos amarelos e, com isso, a área [tex]A_{la}[/tex] de cada losango amarelo é dada por:
[tex]\qquad A_{la}=\dfrac{810}{27}[/tex]
[tex]\qquad A_{la}=30\,\text{cm}^2 [/tex].
Portanto, a área colorida de amarelo mede [tex]6 \times 30[/tex], ou seja, [tex]\fcolorbox{black}{#eee0e5}{$180\,\text{cm}^2$}.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
