Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
Uma bobina com diâmetro interno de [tex]12\, \text{cm}[/tex] ficou com um diâmetro externo (máximo) de [tex]20\, \text{cm}[/tex], depois que nela foi enrolada uma longa faixa de papel com espessura de [tex]0,01\, \text{cm}[/tex], para produzir um "rolo de papel-toalha".
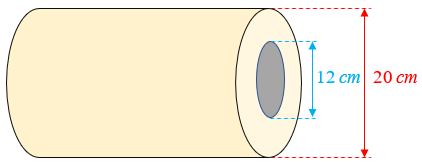
Qual é o comprimento da faixa de papel que foi enrolada?

Ajuda
A soma dos [tex]t[/tex] primeiros números naturais não nulos é dada por
[tex]\qquad \qquad \boxed{1+2+3+ \cdots+t=\dfrac{(1+t)\cdot t}{2}}[/tex]. (Se precisar, visite esta página.)
Solução
A bobina tem um diâmetro interno de [tex]12\, \text{cm}[/tex] e um diâmetro externo máximo de [tex]20\, \text{cm}[/tex]. Assim, quando vista de lado, a espessura da faixa de papel enrolada na bobina é de [tex]\dfrac{20}{2}-\dfrac{12}{2}=4\, \text{cm}[/tex], conforme podemos visualizar na figura a seguir.
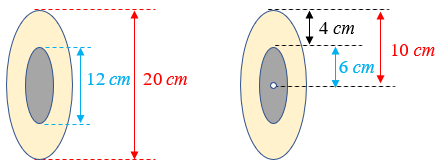
A partir da espessura de [tex]0,01\, \text{cm}[/tex] do papel, precisamos calcular quantas voltas foram dadas no "tubo interno " da bobina para que o "tubo" resultante do papel enrolado tenha a espessura de [tex]4\, \text{cm}.[/tex] Olhando a base do tubo de papel de frente, é como se abríssemos um anel de papel, conseguindo um trapézio de altura [tex]4\, \text{cm}[/tex], formado por várias camadas: cada camada corresponde a uma volta do papel na bobina.
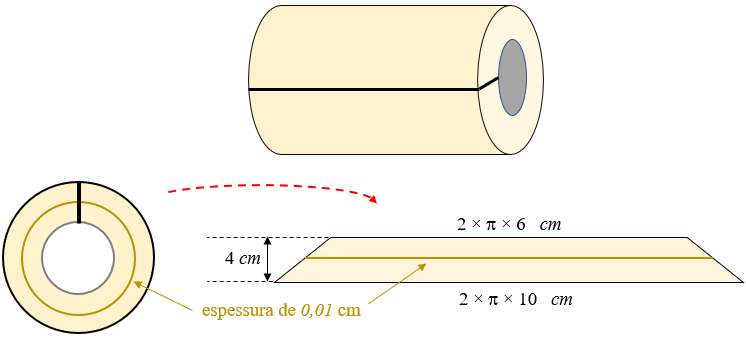
Indicando o número de voltas que produz a espessura de [tex]4\, \text{cm}[/tex] por [tex]n[/tex], vamos fazer os cálculos utilizando uma regra de três:
[tex] \begin{array}{c c c}
\text{espessura}&\text{————–}&\text{voltas ou camadas}\\
0,01\, \text{cm}&\text{————–}&1\\
4\, \text{cm}&\text{————–}& n
\end{array}[/tex]
Assim,
[tex]\qquad 4 \times 1=0,01 \times n \\
\qquad n=\dfrac{4}{0,01}=400 \text{ voltas ou camadas}.[/tex]
Agora, para calcular o comprimento da faixa de papel que foi enrolada, imagine que você pegou faixa de papel de espessura [tex]0,01\, \text{cm}[/tex] e foi enrolando em um cilindro de raio [tex]6\, \text{cm}[/tex] até completar [tex]400[/tex] voltas o que resultou em tubo de papel de espessura [tex]4\, \text{cm}[/tex]. Assim, o comprimento total da faixa de papel é a soma do comprimento de cada uma das [tex]400[/tex] voltas que foram dadas.
Mas é importante você perceber que cada volta tem um raio diferente: é o raio da volta anterior, acrescido dos [tex]0,01\, \text{cm}[/tex] de espessura do papel. Veja:
[tex] \begin{array}{c c l}
\text{volta}&\, \, \, &\text{raio}\\
\hline
1 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &6 \text{( raio interno da bobina)}\\
2 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &6+0,01=6,01=(6+\frac{1}{100})\\
3 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &6,01+0,01=6,02 =(6+\frac{2}{100})\\
4 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &6,02+0,01=6,03 =(6+\frac{3}{100})\\
\vdots &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &\vdots\\
100 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &6,99 =(6+\frac{99}{100})\\
\vdots &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &\vdots\\
200 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &7,99 =(6+\frac{199}{100})\\
\vdots &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &\vdots\\
300 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &8,99 =(6+\frac{299}{100})\\
\vdots &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &\vdots\\
399 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &9,98 =(6+\frac{398}{100})\\
400 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &9,99 =(6+\frac{399}{100})\\
\end{array}[/tex]
Conhecido o raio de cada volta, podemos calcular o comprimento da faixa de papel nela utilizado: o comprimento da faixa de papel em cada volta será o comprimento da circunferência com o raio dessa volta. Lembrando que o comprimento de uma circunferência de raio [tex]r[/tex] é [tex]\boxed{2\cdot \pi \cdot r}[/tex], podemos obter o comprimento em cada volta.
[tex] \begin{array}{c c l}
\text{volta}&\, \, \, &\text{comprimento em cm}\\
\hline
1 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &2\cdot \pi \cdot 6\\
2 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &2\cdot \pi \cdot \left(6+\frac{1}{100}\right)\\
3 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &2\cdot \pi \cdot \left(6+\frac{2}{100}\right)\\
4 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &2\cdot \pi \cdot \left(6+\frac{3}{100}\right)\\
5 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &2\cdot \pi \cdot \left(6+\frac{4}{100}\right)\\
\vdots &\, \, \, \, \, \, \, \, \, \, \, \, \, \, &\vdots\\
399 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, & 2\cdot \pi \cdot \left(6+\frac{398}{100}\right)\\
400 &\, \, \, \, \, \, \, \, \, \, \, \, \, \, & 2\cdot \pi \cdot \left(6+\frac{399}{100}\right)\\
\end{array}[/tex]
Finalmente, vamos somar todos os comprimentos das voltas para determinarmos o comprimento total [tex]C_t[/tex] da faixa de papel que foi enrolada.
[tex]\qquad C_t=2\cdot \pi \cdot 6+2\cdot \pi \cdot \left(6+\frac{1}{100}\right)+2\cdot \pi \cdot \left(6+\frac{2}{100}\right)+2\cdot \pi \cdot \left(6+\frac{3}{100}\right)+\\
\qquad \qquad+2\cdot \pi \cdot \left(6+\frac{4}{100}\right)+\cdots+2\cdot \pi \cdot \left(6+\frac{399}{100}\right)[/tex]
[tex]\qquad C_t=2\cdot \pi \cdot \left(6+ \left(6+\frac{1}{100}\right)+\left(6+\frac{2}{100}\right)+\left(6+\frac{3}{100}\right)+\\
\qquad \qquad +\left(6+\frac{4}{100}\right)+\cdots+\left(6+\frac{399}{100}\right)\right)[/tex]
[tex]\qquad C_t=2\cdot \pi \cdot \left(400 \cdot 6+ \left(\frac{1}{100}+\frac{2}{100}+\frac{3}{100}+\frac{4}{100}+\cdots+\frac{399}{100}\right)\right)[/tex]
[tex]\qquad C_t=2\cdot \pi \cdot \left(2400 +\dfrac{1}{100}\cdot \left(1+2+3+4+\cdots+399\right)\right).[/tex]
Pela fórmula do Lembrete,
[tex]\qquad 1+2+3+4+\cdots+399=\dfrac{(1+399)\cdot 399}{2}=79800[/tex],
logo:
[tex]\qquad C_t=2\cdot \pi \cdot \left(2400 +\dfrac{1}{100}\cdot 79800\right)[/tex]
[tex]\qquad C_t=2\cdot \pi \cdot \left(2400 + 798\right)[/tex]
[tex]\qquad C_t=2\cdot \pi \cdot 3198[/tex]
[tex]\qquad C_t=6396\cdot \pi.[/tex]
Portanto, o comprimento da faixa de papel que foi enrolada é [tex]\fcolorbox{black}{#eee0e5}{$6396 \pi\, \text{cm}$}\, [/tex] ou aproximadamente [tex]\fcolorbox{black}{#eee0e5}{$20\, 083\, \text{cm}$}\, .[/tex]
O esquema de conversão abaixo permite concluir que o comprimento da faixa de papel é aproximadamente [tex]\fcolorbox{black}{#eee0e5}{$201 \text{ metros}$}.[/tex]
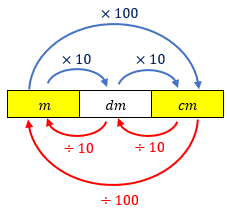
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
