Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
(CEFET-AL – 2013 – IF-AL – Adaptado) Todas as afirmações abaixo são relacionadas a números primos.
[tex]\textcolor{#800000}{(i)} [/tex] Dado um número primo, existe sempre um número primo maior que ele.
[tex]\textcolor{#800000}{(ii)} [/tex] Se dois números naturais não têm fatores primos iguais, então um deles é ímpar.
[tex]\textcolor{#800000}{(iii)} [/tex] Um número primo é sempre ímpar.
[tex]\textcolor{#800000}{(iv)} [/tex] O produto de três números naturais consecutivos é múltiplo de um primo.
[tex]\textcolor{#800000}{(v)} [/tex] A soma de três números naturais consecutivos é múltiplo de três, e três é primo.
- Verifique quais dessas afirmações são verdadeiras.
AJUDA
Quando um número natural [tex] \, n[/tex], [tex] \, n>1[/tex], possui como divisores naturais apenas ele próprio e a unidade, dizemos que [tex] \, n \, [/tex] é um número primo. Desta forma, são números primos: [tex]2[/tex], [tex]3[/tex], [tex]5[/tex], [tex]7[/tex], [tex]11[/tex], [tex]13[/tex], entre muitos outros.
"Existem infinitos números primos" e isto pode ser demonstrado. (Neste momento, estamos interessados apenas no resultado e não em sua demonstração.) O primeiro matemático a demonstrar esse fato foi Euclides (matemático grego cuja biografia você pode encontrar na Biblioteca dos Clubes).
Outra característica importante dos números primos é que eles funcionam como blocos numéricos fundamentais, sendo responsáveis por gerar todos os números naturais diferentes de [tex]0[/tex] e de [tex]1[/tex]". Esta propriedade é conhecida como Teorema Fundamental da Aritmética e ela garante que "um número natural diferente de [tex]0[/tex] e de [tex]1[/tex] ou é um número primo ou pode ser escrito de forma única, a menos da ordem dos fatores, como produto de números primos". (Neste momento, também não estamos interessados na demonstração desse resultado. Mas se você se interessou por esse Teorema, temos uma Sala aqui no Blog dedicada a ele. Você pode visitá-la mais tarde: é só clicar AQUI.)
 |
O vídeo abaixo também pode ajudar… |
Solução
Vamos analisar uma a uma as cinco afirmações.
[tex]\textcolor{#800000}{(i)} [/tex] Dado um número primo, existe sempre um número primo maior que ele.
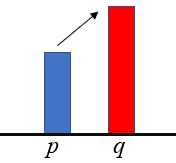
Esta afirmação garante que, dado um número primo [tex]p[/tex], existe sempre um número primo [tex]q[/tex] tal que [tex]q \gt p.[/tex]
Se ela não fosse verdadeira, existiria um número primo [tex]k[/tex] tal que nenhum primo seria maior do que ele. Nesse caso, [tex]k[/tex] seria o maior dentre todos os números primos e, portanto, teríamos no máximo [tex]k[/tex] números primos. (As ilustrações abaixo talvez possam lhe ajudar a entender essa argumentação…)
Mas essa conclusão contrariaria o fato de existirem infinitos números primos, não é?
Dessa forma, a afirmação [tex]\textcolor{#800000}{(i)} [/tex] não pode ser falsa.
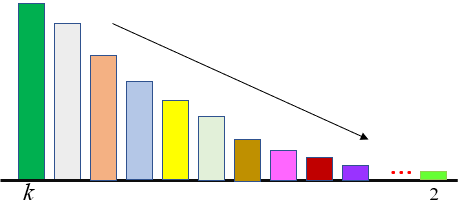
Pelo exposto, garantimos que:
a afirmação [tex]\textcolor{#800000}{(i)} [/tex] é VERDADEIRA.
[tex]\textcolor{#800000}{(ii)} [/tex] Se dois números naturais não têm fatores primos iguais, então um deles é ímpar.
- Ambos são pares.
- Ambos são ímpares.
- Um é par e o outro é ímpar.
Mas se soubermos que dois números não têm fatores primos iguais, eles não podem ser simultaneamente pares, pois, se o fossem, eles teriam o [tex]2[/tex] como fator primo comum. Nesse caso, das três condições acima apenas uma das seguintes é verdadeira:
- Ambos são ímpares.
- Um é par e o outro é ímpar.
Portanto, se dois números não têm fatores primos iguais, então pelo menos um deles será ímpar.
Pelo exposto, garantimos que:
a afirmação [tex]\textcolor{#800000}{(ii)} [/tex] é VERDADEIRA.
[tex]\textcolor{#800000}{(iii)} [/tex] Um número primo é sempre ímpar.
Sabemos que o número [tex]2[/tex] é divisível apenas por ele próprio e por [tex]1.[/tex] Assim, [tex]2[/tex], que não é um número ímpar, é um número primo.
Portanto:
a afirmação [tex]\textcolor{#800000}{(iii)} [/tex] é FALSA.
[tex]\textcolor{#800000}{(iv)} [/tex] O produto de três números naturais consecutivos é múltiplo de um primo.
Seja [tex]a[/tex] um produto de três números naturais consecutivos. Assim, existe um número natural [tex]n[/tex] tal que [tex]a=n \cdot (n+1) \cdot (n+2).[/tex]
- Se [tex]a=0[/tex], [tex]a[/tex] é múltiplo de qualquer número natural, em particular de um primo.
- Se [tex]a [/tex] for não nulo, então [tex]n\geqslant 1[/tex], [tex]n+1\gt 1[/tex] e [tex]n+2\gt 1[/tex], donde [tex]a=n \cdot (n+1) \cdot (n+2)\gt 1[/tex]. Pelo Teorema Fundamental da Aritmética, como [tex]a\gt 1[/tex], ou [tex]a[/tex] é um número primo ou [tex]a[/tex] pode ser escrito como produto de números primos.
- como todo número é múltiplo de si próprio, se [tex]a[/tex] for um número primo ele é múltiplo de um primo;
- se [tex]a[/tex] for escrito como produto de números primos, em particular, ele é múltiplo de um primo.
Mas:
De todo modo, um produto não nulo de três números naturais consecutivos é múltiplo de um primo.
De qualquer forma:
a afirmação [tex]\textcolor{#800000}{(iv)} [/tex] é VERDADEIRA.
[tex]\textcolor{#800000}{(v)} [/tex] A soma de três números naturais consecutivos é múltiplo de três, e três é primo.
Seja [tex]n[/tex] um número natural qualquer e sejam seus consecutivos [tex]n+1[/tex] e [tex]n+2.[/tex]
Observe que:
[tex]\qquad x=n+(n+1)+ (n+2)=3n+3=3\cdot(n+1)[/tex],
ou seja, [tex]x[/tex] é um múltiplo de [tex]3[/tex].
Como [tex]3[/tex] é um número primo, concluímos que
a afirmação [tex]\textcolor{#800000}{(v)} [/tex] é VERDADEIRA.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
