(A) Problema para ajudar na escola: Catetos de um triângulo retângulo

Clique no botão abaixo para visualizar o problema.

Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio )

Em um dado triângulo retângulo, a hipotenusa mede [tex]25 \, \text{cm}[/tex] e a altura relativa a ela mede [tex]12 \, \text{cm}\, .[/tex]
Qual é a medida de cada cateto desse triângulo?

Lembretes

Vamos resolver este problema utilizando apenas resultados bem conhecidos da Geometria:
✐ Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.

✐ Área do triângulo:[tex]\dfrac{\text{base $\times$ altura}}{2}[/tex]

Solução

Vamos supor que os catetos de um triângulo retângulo cuja hipotenusa mede [tex]25 \, \text{cm}[/tex] e a altura relativa a ela mede [tex]12 \, \text{cm}\, [/tex] tenham comprimentos [tex]a \, \text{cm}[/tex] e [tex]b \, \text{cm}[/tex], conforme vemos na figura abaixo.

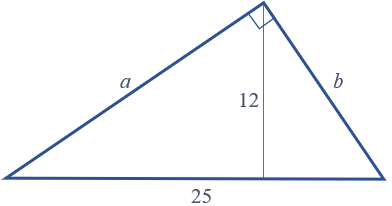
Pelo segundo Lembrete, a área de um triângulo é dada pela metade do produto entre uma base e sua respectiva altura. No caso do nosso triângulo, vamos calcular a sua área de dois modos:

utilizando os dados do problema: [tex]\frac{25 \times 12}{2}[/tex],
considerando como base e altura os dois catetos, já que o triângulo é retângulo: [tex]\frac{a \times b}{2}[/tex].

Dessa forma, se [tex]A_t[/tex] é a área do nosso triângulo, então:
[tex]\qquad A_t=\dfrac{25 \times 12}{2}=\dfrac{a \times b}{2}[/tex],
e assim temos que:
[tex]\qquad a \times b=300.\qquad \textcolor{#800000}{(i)}[/tex]
Por outro lado, o primeiro Lembrete nos assegura que
[tex]\qquad a^2+b^2=625.\qquad \textcolor{#800000}{(ii)}[/tex]
A partir das equações [tex]\textcolor{#800000}{(i)} \, [/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], podemos resolver algebricamente o problema de duas maneiras; observe.

Multiplicando a equação [tex]\textcolor{#800000}{(i)} \, [/tex] por [tex]2[/tex], temos que

[tex]\quad 2\times a \times b=600.\qquad \textcolor{#800000}{(iii)}[/tex]
Logo, somando [tex]\textcolor{#800000}{(ii)} \, [/tex] e [tex]\textcolor{#800000}{(iii)}[/tex], segue que:
[tex]\quad \left(a^2+b^2\right)+2\times a \times b=625+600[/tex]
[tex]\quad a^2+2\times a \times b+b^2=1225[/tex]
[tex]\quad \left(a+b\right)^2=1225[/tex]
[tex]\quad \sqrt{ \left(a+b\right)^2}=\sqrt{1225}=35.[/tex]
Como [tex]a \, [/tex] e [tex] \, b[/tex] são números positivos, então [tex]a+b=35[/tex],
donde
[tex]\quad b=35-a.\qquad \textcolor{#800000}{(iv)}[/tex],
Substituindo [tex]\textcolor{#800000}{(iv)} \, [/tex] em [tex]\textcolor{#800000}{(i)} \, [/tex], obtemos:
[tex]\quad 35a-a^2=300[/tex]
[tex]\quad a^2-35a+300=0.[/tex]
Resolvendo essa equação do segundo grau obtemos as raízes:
[tex]\quad a=\dfrac{35\pm\sqrt{1225-1200}}{2}=\dfrac{35\pm 5}{2}[/tex]
[tex]\quad a_1=\dfrac{35+5}{2}=20 \qquad [/tex] e [tex]\qquad a_2=\dfrac{35-5}{2}=15 \, [/tex].
Substituindo essas raízes em [tex]\textcolor{#800000}{(iv)} \, [/tex], obtemos os respectivos valores para o comprimento do segundo cateto:
[tex]\quad b_1=35-a_1=35-20=15 \, \, [/tex] e
[tex]\quad b_2=35-a_2=35-15=20 \, \, \, .[/tex]
Com isso, o triângulo retângulo em questão tem catetos com comprimentos [tex] \, \fcolorbox{black}{#eee0e5}{$15 \, \text{cm}\text{ e } 20 \, \text{cm}$} \, .[/tex]

Podemos trabalhar diretamente com as equações [tex]\textcolor{#800000}{(i)} \, [/tex] e [tex] \, \textcolor{#800000}{(ii)} \, .[/tex]

De [tex]\textcolor{#800000}{(i)} \, [/tex], como [tex]b\ne 0[/tex], segue que
[tex]\quad a=\dfrac{300}{b}.\qquad \textcolor{#800000}{(v)}[/tex]
Substituindo [tex]\textcolor{#800000}{(v)} \, [/tex] em [tex]\textcolor{#800000}{(i)} \, [/tex], obtemos a equação biquadrada
[tex]\quad b^4-625b^2+90000=0.\qquad \textcolor{#800000}{(vi)}[/tex]
Se fizermos [tex]x=b^2[/tex] em [tex]\textcolor{#800000}{(vi)} \, [/tex], obtemos a seguinte equação do segundo grau em [tex]x[/tex]:
[tex]\quad x^2-625x+90000=0[/tex]
Resolvendo essa equação obtemos as raízes:
[tex]\quad x=\dfrac{625\pm\sqrt{390625-360000}}{2}\\
\quad x=\dfrac{625\pm 175}{2}[/tex]
[tex]\quad x_1=\dfrac{625+175}{2}=400 \;[/tex] e [tex]\;x_2=\dfrac{625-175}{2}=225 \, [/tex].
Mas [tex]x=b^2[/tex], logo:
[tex]\quad b_1^2=400 \qquad [/tex] e [tex]\qquad b_2^2=225 \, [/tex].
Como estamos lidando com medidas, [tex] \, b_1 \gt 0[/tex] e [tex] \, b_2 \gt 0[/tex], e
[tex]\quad b_1=20 \qquad [/tex] e [tex]\qquad b_2=15 \, .[/tex]
Substituindo esses valores em [tex]\textcolor{#800000}{(v)} \, [/tex], obtemos os respectivos valores para o comprimento do outro cateto:
[tex]\quad a_1=\dfrac{300}{b_1}=\dfrac{300}{20}=15\qquad [/tex] e
[tex]\, \\
\qquad a_2=\dfrac{300}{b_1}=\dfrac{300}{15}=20.[/tex]
Com isso, o triângulo retângulo em questão tem catetos com comprimentos [tex] \, \fcolorbox{black}{#eee0e5}{$15 \, \text{cm}\text{ e } 20 \, \text{cm}$} \, .[/tex]

Solução elaborada pelos Moderadores do Blog.

Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo.
Você pode abrir o arquivo diretamente no seu navegador (Chrome, Edge, Firefox, Safari, entre outros), mas também pode utilizar o software gratuito Adobe Acrobat Reader.
Caso o dispositivo que você está utilizando não tenha o Acrobat Reader instalado, é só clicar AQUI para fazer o download adequado ao seu dispositivo.

Arquivo