Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
(Adaptado da Junior Mathematical Olympiad – 2014) Um ponto [tex]P[/tex] tomado no interior de um paralelogramo [tex]ABCD [/tex] define os triângulos [tex]APB [/tex], [tex]BPC [/tex], [tex]CPD [/tex] e [tex]DPA[/tex].
Que relação existe entre as áreas desses quatro triângulos? Justifique sua resposta.

Uma ajuda
O applet abaixo pode ajudar…
Para utilizá-lo, basta movimentar o ponto [tex]P[/tex].
Observe que [tex]V[/tex] denota a soma das áreas dos triângulos coloridos de verde e [tex]L[/tex] denota a soma das áreas dos triângulos coloridos com a cor alaranjada.
OBMEP_srg, criado com o GeoGebra

Um lembrete
Cada diagonal de um paralelogramo divide-o em dois triângulos congruentes, ou seja, em dois triângulos com a mesma área.
Solução
Tome um ponto [tex]P[/tex] no interior de um paralelogramo [tex]ABCD [/tex], conforme ilustra a figura abaixo. Denominaremos as áreas dos triângulos [tex]APB [/tex], [tex]BPC [/tex], [tex]CPD [/tex] e [tex]DPA[/tex] por [tex]\textcolor{#009900}T[/tex], [tex]\textcolor{#ff6600}M[/tex], [tex]\textcolor{#FFD700}H[/tex] e [tex]\textcolor{#CC66FF}E[/tex], respectivamente.
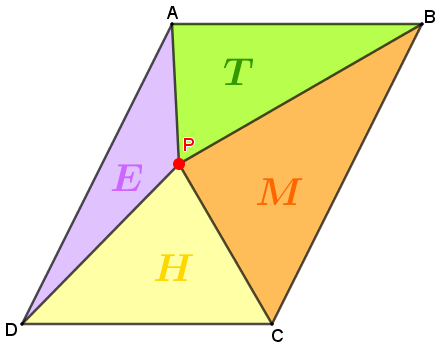
Utilizando o applet, podemos perceber que [tex]\boxed{\textcolor{#009900}{T}+\textcolor{#FFD700}{H}=\textcolor{#CC66FF}{E}+\textcolor{#ff6600}{M}}[/tex], e é essa relação que vamos provar.
Com efeito, ao traçarmos dois segmentos passando por [tex]P[/tex] e paralelos, respectivamente, aos lados [tex]\overline{AB} \, [/tex] e [tex] \, \overline{AD}[/tex] do paralelogramo [tex]ABCD [/tex], obtemos quatro paralelogramos que decompõem cada um dos triângulos [tex]APB [/tex], [tex]BPC [/tex], [tex]CPD [/tex] e [tex]DPA[/tex] em dois triângulos, cujas áreas denotaremos por [tex]\textcolor{#009900}{T_1}[/tex], [tex]\textcolor{#009900}{T_2}[/tex], [tex]\textcolor{#ff6600}{M_1}[/tex], [tex]\textcolor{#ff6600}{M_2}[/tex], [tex]\textcolor{#FFD700}{H_1}[/tex], [tex]\textcolor{#FFD700}{H_2}[/tex], [tex]\textcolor{#CC66FF}{E_1}[/tex] e [tex]\textcolor{#CC66FF}{E_2}[/tex], conforme ilustra a próxima figura.
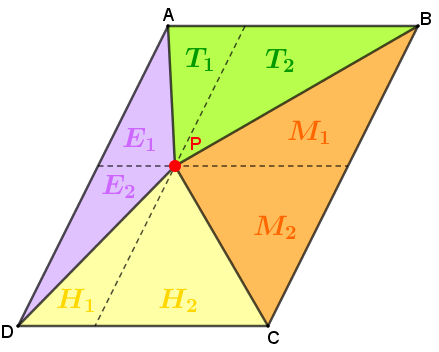
Perceba que os segmentos [tex]\overline{AP} \, [/tex], [tex]\overline{BP} \, [/tex], [tex]\overline{CP} \, [/tex] e [tex]\overline{DP} \, [/tex] são diagonais dos quatro paralelogramos obtidos; assim, pelo Lembrete, temos que:
- [tex]\textcolor{#CC66FF}{E_1}=\textcolor{#009900}{T_1}[/tex];
- [tex]\textcolor{#009900}{T_2}=\textcolor{#ff6600}{M_1}[/tex];
- [tex]\textcolor{#ff6600}{M_2}=\textcolor{#FFD700}{H_2}[/tex];
- [tex]\textcolor{#FFD700}{H_1}=\textcolor{#CC66FF}{E_2}.[/tex]
Dessa forma:
[tex]\qquad \qquad \begin{align*}\textcolor{#009900}{T}+\textcolor{#FFD700}{H}&=\left(\textcolor{#009900}{T_1}+\textcolor{#009900}{T_2}\right)+\left(\textcolor{#FFD700}{H_1}+\textcolor{#FFD700}{H_2}\right)\\
&=\left(\textcolor{#CC66FF}{E_1}+\textcolor{#ff6600}{M_1}\right)+\left(\textcolor{#CC66FF}{E_2}+\textcolor{#ff6600}{M_2}\right)\\
&=\left(\textcolor{#CC66FF}{E_1}+\textcolor{#CC66FF}{E_2}\right)+\left(\textcolor{#ff6600}{M_1}+\textcolor{#ff6600}{M_2}\right)\\
&=\textcolor{#CC66FF}{E}+\textcolor{#ff6600}{M}
\end{align*}[/tex]
Portanto, de fato, [tex] \, \fcolorbox{black}{#eee0e5}{$T+H=E+M$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
