Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Difícil)
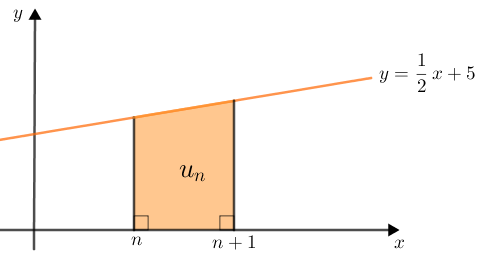
Na figura, para cada número natural [tex]n[/tex], [tex]u_n[/tex] é a área colorida abaixo da reta definida por [tex]y=\frac{1}{2}x+5.[/tex]
(a) Calcule [tex]u_n[/tex], em função de [tex]n[/tex].
(b) Determine [tex]u_0[/tex] e interprete geometricamente a região que tem essa área.
(c) A sequência [tex]\{u_0, \, u_1, \, u_2, \, \cdots \, , \, u_n \, \cdots \, \}[/tex] é uma PG? É uma PA?
Solução
(a) Seja [tex]n[/tex] um número natural.
Considere a função [tex]f:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]f(x)=\frac{1}{2}x+5[/tex], cujo gráfico é a reta [tex]y=\frac{1}{2}x+5[/tex] destacada na figura mostrada no enunciado.
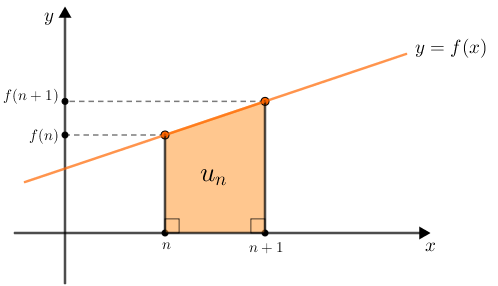
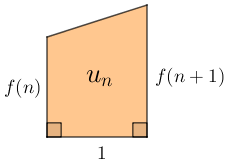
Dessa forma, fixadas uma unidade de comprimento e uma unidade de área, temos que [tex]u_n[/tex] é a área de um trapézio retângulo de altura [tex]1[/tex] e cujos comprimentos das bases menor e maior são, respectivamente, [tex]f(n)[/tex] e [tex]f(n+1) \, .[/tex]
Com isso, sabendo que [tex]f(x)=\frac{1}{2}x+5=\dfrac{x+10}{2}[/tex], segue que:
[tex]\qquad u_n=\dfrac{\left(\text{base maior} + \text{base menor}\right) \times \text{altura}}{2}[/tex]
[tex]\qquad u_n=\dfrac{\left(f(n+1) + f(n)\right) \times 1}{2}[/tex]
[tex]\qquad u_n=\dfrac{f(n+1) + f(n)}{2}[/tex]
[tex]\qquad u_n=\dfrac{\dfrac{(n+1)+10}{2} + \dfrac{n+10}{2}}{2}[/tex]
[tex]\qquad u_n=\dfrac{n+1+10+n+10}{4}[/tex]
[tex]\qquad u_n=\dfrac{2n+21}{4} \, [/tex] unidades de área.
Portanto, para um número natural [tex]n[/tex], temos que [tex] \, \fcolorbox{black}{#fda}{$ u_n=\dfrac{2n+21}{4}$} \, .[/tex]
(b) Para [tex]n=0[/tex], temos que [tex] \, u_0=\dfrac{0+21}{4} \, [/tex] e, assim, [tex] \, \fcolorbox{black}{#fda}{$ u_0=\dfrac{21}{4}$} \, [/tex] unidades de área.
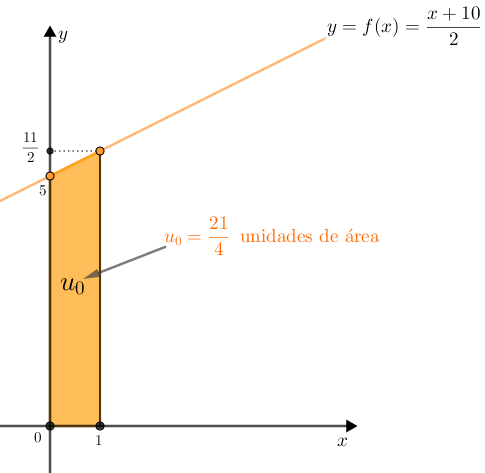
Essa é a área do trapézio retângulo de altura [tex]1[/tex] e cujos comprimentos das bases menor e maior são, respectivamente, [tex]f(0)=5[/tex] e [tex]f(1)=\dfrac{11}{2} \, [/tex]. Conforme mostrado na figura a seguir, esse trapézio fica perfeitamente definido pela reta dada pela equação [tex]y=\frac{1}{2}x+5[/tex], pelo eixo [tex]x[/tex], pelo eixo [tex]y \, [/tex] e pela reta dada pela equação [tex]y=1[/tex].
(c) Vamos observar a sequência [tex]\{u_0; \, u_1; \, u_2; \, \cdots \, ; \, u_n \, ; \, u_{n+1}; \, \cdots \, \}[/tex]:
[tex]\qquad \{u_0=\dfrac{21}{4}; \, u_1=\dfrac{23}{4}; \, u_2=\dfrac{25}{4}; \, \cdots \, ; \, u_n=\dfrac{2n+21}{4}; \, u_{n+1}=\dfrac{2n+23}{4}; \cdots \, \}.[/tex]
Perceba que:
- [tex]\dfrac{u_{n+1}}{u_n}=\dfrac{\frac{2n+23}{4}}{\frac{2n+21}{4}}=\dfrac{2n+23}{2n+21}[/tex]
- [tex]u_{n+1}-u_n=\dfrac{2n+23}{4}-\dfrac{2n+21}{4}=\dfrac{2n+23-2n-21}{4}=\dfrac{2}{4}=\dfrac{1}{2}[/tex].
Assim,
- como [tex]\dfrac{u_{n+1}}{u_n}[/tex] não é uma constante (a razão depende de [tex]n[/tex]), então a sequência [tex]\{u_0; \, u_1; \, u_2; \, \cdots \, ; \, u_n \, ; \, u_{n+1}; \, \cdots \, \}[/tex] não é uma Progressão Geométrica.
- como [tex]u_{n+1}-u_n[/tex] é uma constante, então a sequência [tex]\{u_0; \, u_1; \, u_2; \, \cdots \, ; \, u_n \, ; \, u_{n+1}; \, \cdots \, \}[/tex] é uma Progressão Aritmética.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
