A Regra de Três é um processo matemático utilizado na resolução de muitos problemas que envolvem duas ou mais grandezas diretamente ou inversamente proporcionais. Com esse processo conseguimos determinar um valor desconhecido, a partir de outros três conhecidos – daí vem o nome da regra.
Ao longo da história, encontramos indícios de que esse processo tenha sido utilizado em atividades práticas por civilizações da antiguidade e, muito provavelmente, essa utilização teve origem na China antiga.
No papiro de Ahmes (ou Rhind), documento egípcio datado de cerca de 1650 a.C., foram encontrados problemas cujas manipulações feitas nas suas resoluções equivalem à hoje conhecida como Regra de Três.
O nome Regra de Três apareceu explicitamente na Índia. No livro Aryabhatiya de 499 do matemático indiano Aryabhata (476 – 550), aparecem, além da Regra de Três, as regras de cinco, de sete e outros casos especiais.
O matemático árabe al-Kwarizimi (680 – 750) a utilizava na solução de problemas de transações comerciais, ressaltando a relação de proporcionalidade entre quatro números: medida e preço, quantidade e soma. Mesmo fazendo uso da regra, o também matemático árabe al-Karaji (953 – 1029) se referia a ela apenas como “multiplicação e divisão”.
A Regra de Três recebeu vários nomes na sua trajetória histórica, como os registados com suas respectivas traduções na imagem a seguir.
 Imagem adaptada de “Uma sequência didática para o ensino de Regras de Três”.
Imagem adaptada de “Uma sequência didática para o ensino de Regras de Três”.
A regra de três entrou na Europa via o livro Liber Abaci do matemático italiano Leonardo Fibonacci (1170 – 1250), mas a sua relação com a álgebra foi fortemente enfatizada pela primeira vez pelo algebrista alemão Michael Stifel (1487-1567).
A utilização da regra de três simples é fundamental para descobrirmos um valor não identificado, por meio de outros três valores conhecidos no problema que se deseja resolver; mais especificamente,
Regra de três simples é um processo prático utilizado na resolução de problemas de proporcionalidade que envolvem duas grandezas, cada uma apresentando dois valores. Teremos, então, quatro valores dos quais três são apresentados no problema e, portanto, conhecidos, e o quarto será determinado. Devemos, então, determinar esse valor com base nos outros três já conhecidos.
Passos para se resolver uma regra de três simples:
2º) Construir uma tabela com duas colunas, “agrupando, em cada coluna, os valores da mesma grandeza” e “mantendo, na mesma linha, os valores de grandezas diferentes que estão em correspondência”. Assim, colocaremos na tabela os dados que o problema nos fornece: os três valores conhecidos serão colocados explicitamente e o valor desconhecido será representado por uma letra.
3º) Identificar se as duas grandezas são diretamente ou inversamente proporcionais. Para isso devemos observar se, quando os valores de uma grandeza aumentam, os respectivos valores da outra grandeza aumentam ou diminuem proporcionalmente.
4º) Montar uma equação de acordo com o tipo de proporcionalidade identificado no passo anterior e resolver a equação.
Vejamos alguns exemplos:
Qual a massa corporal do filho, sabendo que a mãe ministrou corretamente 30 gotas do remédio a seu filho a cada 8 horas?
Solução:
1º) Note que o intervalo de tempo de 8 horas é um dado não muito relevante na resolução do problema, uma vez que o intervalo não se altera, ou seja, o medicamento sempre será ministrado para o menino a cada 8 horas. Assim, temos apenas duas grandezas envolvidas que serão úteis na resolução do problema: massa corporal e dosagem.
2º) Foram dados três números e deseja-se o quarto, que corresponde à massa corporal do filho, sabendo que ele tomou 30 gotas do medicamento. Então, podemos criar a seguinte tabela de dados:

3º) Como foi indicado que o menino deveria tomar 5 gotas para cada 2 kg de massa corporal, então, à medida que a massa aumenta, a quantidade de gotas que devem ser ministradas também aumenta, na mesma proporção, o que implica que as grandezas envolvidas são diretamente proporcionais.

As duas setas com sentido “para cima”, na tabela acima, indicam que as grandezas são diretamente proporcionais, pois quanto maior a massa corporal, maior deverá ser o número de gotas. Claramente, quanto menor a massa corporal, menor o número de gotas, então, na tabela, as setas que aparecem orientadas “para cima”, poderiam muito bem estar orientadas “para baixo”, e as grandezas seriam diretamente proporcionais da mesma forma.
4º) Agora, vamos montar a equação de proporcionalidade. Para isso, podemos estabelecer que o sentido de uma seta leva a orientação de escrita da respectiva fração. Dessa forma, como na última tabela ambas as setas estão orientadas “para cima”, então os numeradores e denominadores das frações serão, respectivamente, os valores da segunda linha e primeira linha:
[tex]\qquad \dfrac{x}{2} = \dfrac{30}{5}.[/tex]
“Multiplicando cruzado”, segue que:
[tex]\qquad 5x = 2\times 30\\
\qquad \boxed{x = 12}.\\
[/tex]
Portanto, a massa corporal do menino corresponde a 12 kg.
Antes de irmos para o próximo problema, vamos estabelecer uma maneira de identificar visualmente se duas grandezas são diretamente ou inversamente proporcionais utilizando as setas que fizemos no terceiro passo do exemplo anterior:
► Se ambas as setas ficarem orientadas ou “para cima” ou “para baixo”, então as grandezas são diretamente proporcionais;
► Se as setas ficarem com sentidos contrários, então as grandezas são inversamente proporcionais.
Solução:
1º) As duas grandezas envolvidas no problema são tempo e quantidade de ralos.
2º) Foram dados três números e deseja-se o quarto, que corresponde à quantidade de ralos do novo reservatório, sabendo que este deverá escoar toda a água em 4 horas. Então, podemos criar a seguinte tabela de dados:

3º) Como o novo reservatório de água deve escoar toda a água em um tempo menor do que o do reservatório que já existe, então, obviamente, o novo reservatório deve possuir uma quantidade maior de ralos. Desse modo, à medida que o tempo de escoamento diminui, faz-se necessária uma quantidade maior de ralos, o que implica que as grandezas envolvidas são inversamente proporcionais.
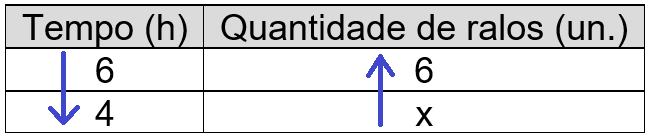
Quanto menor o tempo de escoamento, maior a quantidade de ralos, por isso, na tabela acima, a seta da grandeza “tempo” aparece com sentido para baixo e a seta da grandeza “quantidade de ralos” aparece com sentido para cima. Como as setas têm sentidos contrários, conclui-se que as grandezas são inversamente proporcionais.
4º) Agora, montamos a equação de proporcionalidade escrevendo as frações no sentido em que as setas estão:
[tex]\qquad \dfrac{6}{4} = \dfrac{x}{6}\\
\qquad 4x = 6\times 6\\
\qquad \boxed{x = 9}.\\
[/tex]
Portanto, o novo reservatório deve possuir 9 ralos.
Enquanto a regra de três simples nos limita a resolver problemas que envolvam apenas duas grandezas, a regra de três composta nos permite resolver problemas com mais de duas grandezas.
Regra de três composta é um processo prático utilizado na resolução de problemas de proporcionalidade que envolvem mais de duas grandezas, cada uma dessas grandezas apresentando dois valores. Assim, se o problema envolver [tex]n[/tex] grandezas proporcionais, teremos que lidar com [tex]2n[/tex] valores, valores dos quais [tex]2n-1[/tex] são apresentados explicitamente no problema e um deverá ser determinado.
Passos para se resolver uma regra de três composta:
2º) Construir uma tabela na qual a quantidade de colunas seja igual à quantidade de grandezas, “agrupando, em cada coluna, os valores da mesma grandeza” e “mantendo, na mesma linha, os valores de grandezas diferentes que estão em correspondência”. Assim, colocaremos na tabela os dados que o problema nos fornece: os valores conhecidos serão colocados explicitamente e o valor desconhecido será representado por uma letra.
3º) Identificar se a grandeza com o valor desconhecido é diretamente ou inversamente proporcional a cada uma das outras grandezas. Essas análises entre a grandeza com o valor desconhecido e as demais devem ser feitas uma a uma.
4º) Montar uma equação de acordo com os tipos de proporcionalidade identificados no passo anterior e resolver a equação.
Mas, atenção!
- Em um dos membros da equação a ser obtida, deve ficar apenas a razão dos valores da grandeza na qual está a incógnita.
- Todas as razões obtidas em cada uma das outras grandezas devem aparecer multiplicadas no outro membro da equação.
Vejamos alguns exemplos:
Qual deve ser a nova jornada de trabalho diária dos funcionários para que a empresa consiga atender a demanda?
Solução:
1º) Como podemos perceber, existem três grandezas envolvidas neste problema, sendo elas a quantidade de funcionários, a quantidade de camisetas produzidas diariamente e a jornada de trabalho diária dos funcionários.
2º) Assim, os dados apresentados podem ser agrupados em uma tabela da seguinte maneira:

3º) Vamos agora analisar o tipo de proporcionalidade entre a grandeza “jornada de trabalho” com cada uma das outras grandezas. (Para isso, fixe inicialmente um sentido para a seta da grandeza com o valor desconhecido.)
● Supondo que a quantidade de camisetas produzidas diariamente fosse a mesma, diminuindo-se a jornada de trabalho, a quantidade de funcionários deveria aumentar. Assim, essas duas grandezas são inversamente proporcionais (as setas devem ter sentidos contrários).
● Agora, supondo constante a quantidade de funcionários, diminuindo-se a jornada de trabalho, a quantidade de camisetas produzidas também deveria diminuir. Assim, essas duas grandezas são diretamente proporcionais (as setas devem ter mesmo sentido).
Vejamos a disposição das setas, abaixo:

4º) Vamos montar a equação de proporcionalidade escrevendo as frações no sentido em que as setas estão; lembrando que, conforme foi mencionado logo após os passos de resolução, uma vez que o valor desconhecido pertence à grandeza “jornada de trabalho”, a razão [tex]6/x[/tex] deve aparecer sozinha em um dos membros da equação. Assim, obedecendo o sentido das setas, temos:
[tex]\qquad \dfrac{6}{x} = \dfrac{96}{36}\cdot \dfrac{5400}{21600} \\
\qquad \dfrac{6}{x} = \dfrac{8}{3}\cdot \dfrac{1}{4} \\
\qquad \dfrac{6}{x} = \dfrac{8}{12}\\
\qquad 8x = 72\\
\qquad \boxed{x = 9}.\\
[/tex]
Logo, a jornada de trabalho deve ser aumentada para 9 horas diárias.
Solução:
1º) Como podemos perceber, existem quatro grandezas envolvidas neste problema, sendo elas a quantidade de máquinas, o tempo diário de trabalho das máquinas, a quantidade de peças produzidas e a quantidade de dias de funcionamento das máquinas.
2º) Assim, os dados apresentados podem ser agrupados em uma tabela da seguinte maneira:

3º) Vamos agora analisar o tipo de proporcionalidade entre a grandeza quantidade de peças com cada uma das outras grandezas.
Fixe inicialmente um sentido para a seta da grandeza com o valor desconhecido.
● Supondo que o tempo de funcionamento diário e o total de dias de funcionamento das máquinas fosse constante, o aumento na quantidade de peças produzidas deveria acarretar o aumento do total de máquinas. Assim, essas duas grandezas são diretamente proporcionais (as setas devem ter mesmo sentido).
● Supondo que a quantidade de máquinas e o total de dias de funcionamento das máquinas fosse constante, o aumento na quantidade de peças produzidas deveria acarretar o aumento do tempo de funcionamento diário das máquinas. Assim, essas duas grandezas também são diretamente proporcionais (as setas devem ter mesmo sentido).
● Por fim, se fossem constantes a quantidade de máquinas e o tempo diário de funcionamento das mesmas, o aumento da quantidade de peças produzidas deveria acarretar o aumento também do total de dias. Portanto, essas duas grandezas também são diretamente proporcionais (as setas devem ter mesmo sentido).

4º) Montando a equação, obtemos:
[tex]\qquad \dfrac{x}{600} = \dfrac{12}{5}\cdot \dfrac{10}{8}\cdot \dfrac{5}{1}\\
\qquad \dfrac{x}{600} = \dfrac{600}{40}\\
\qquad 40x = 360 000\\
\qquad \boxed{x = 9000}.\\
[/tex]
Logo, o total de peças produzidas nas novas condições é 9000 peças.
Antes de partirmos para os problemas, deixamos duas observações para reflexão.
I – Habitue-se a analisar se o modelo matemático utilizado em um problema de fato se aplica à situação que foi modelada.
É razoável pensar que, se fossem colocados 3 pedreiros para construí-lo, ele ficaria pronto em um dia.
Também seria razoável pensar que, se fossem colocados 6 pedreiros para construir o muro, ele ficaria pronto em meio dia.
Teoricamente, tudo isso faz sentido pois estamos lidando com duas grandezas inversamente proporcionais: quanto mais pedreiros, menos tempo de construção, não é?
Mas, na prática, não podemos ir aumentando o número de pedreiros para que o muro seja construído em minutos, ou até em poucos segundos…
Não haveria espaço para todos trabalharem…
 Imagem extraída de “Construindo conhecimentos em Matemática”.
Imagem extraída de “Construindo conhecimentos em Matemática”.
Pela matemática, alguém poderia pensar: “mais pessoas trabalhando, significa menos tempo de trabalho”; então, se para este ano fossem liberados 10 funcionários para a montagem do mesmo número de cadernos, o serviço poderia ser concluído em 4 horas.
Mas é praticamente impossível que 10 pessoas mantenham a organização e a eficácia para fazer o serviço em uma sala tão minúscula, não é?
 Imagem extraída de “Matemática hoje é feita assim”.
Imagem extraída de “Matemática hoje é feita assim”.
Particularmente, até quando a proporcionalidade faz sentido?
 Sally Brown, personagem do cartunista Charles Schulz.
Sally Brown, personagem do cartunista Charles Schulz.
II – Lembre-se sempre de não aplicar proporcionalidade em problemas cujas grandezas não se relacionam de fato.

 |
Agora sim!
|
Equipe COM – OBMEP
