Clique no botão abaixo para visualizar o problema.
Problema
Qual seria o comprimento, em quilômetros, do trajeto que:
- sai de um dos Polos terrestres em direção à Linha do Equador, por um meridiano; ao chegar na Linha do Equador, se desloca lateralmente [tex]60^\circ[/tex] para oeste e retorna, por um segundo meridiano, para o Polo inicial?
Para esse problema, suponha que o planeta Terra seja totalmente esférico com raio [tex]R=6300\text{ km}[/tex] e, para efeito de cálculo, utilize [tex]\pi=3,14[/tex].

Ajuda
A um arco de circunferência podemos associar duas medidas distintas:
✐ a sua medida angular (em graus ou radianos), [tex]\alpha[/tex];
✐ a sua medida linear (em unidades de comprimento), [tex]comp[/tex].
Conhecida uma delas, a outra pode ser obtida a partir de uma regra de três simples:
| [tex]2\pi \, r[/tex] | ————————————– | [tex]360^\circ[/tex] |
| [tex]comp[/tex] | ————————————– | [tex]\alpha[/tex] |
Se você não se lembra disso, não faz mal: clique AQUI.
Solução 1
Podemos ilustrar o enunciado do problema com a figura abaixo, sendo o ponto [tex]N[/tex] o polo Norte e o ponto [tex]C[/tex] o centro da esfera (Terra).
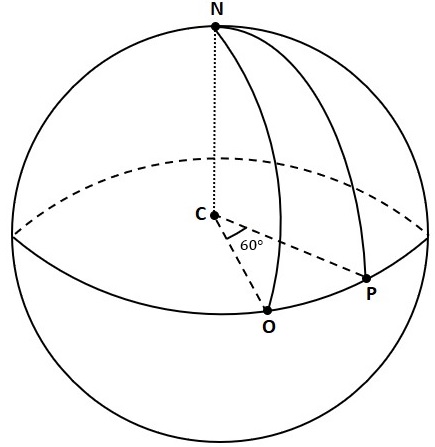
Como o raio da Terra mede [tex]R=6300\text{ km}[/tex], podemos calcular o comprimento [tex]c[/tex] da linha do Equador:
[tex]\qquad c=2 \cdot \pi \cdot R\\
\qquad c=2 \cdot \pi \cdot 6300\\
\qquad c=(12600\cdot \pi) \text{ km}.[/tex]
Do enunciado, temos que a medida do ângulo [tex]O\hat C P~[/tex] é [tex]~60^\circ[/tex]; portanto, usando a Ajuda, podemos calcular o comprimento do arco [tex]\stackrel{\frown}{OP}[/tex]:
| [tex]12600\cdot \pi[/tex] | ————————————– | [tex]360^\circ[/tex] |
| [tex]comp_\stackrel{\frown}{OP}[/tex] | ————————————– | [tex]60^\circ[/tex] |
[tex]\quad comp_\stackrel{\frown}{OP}=\dfrac {60^\circ}{360^\circ}\cdot 12600 \cdot \pi =\dfrac {1}{6}\cdot 12600 \cdot \pi \\
\quad comp_\stackrel{\frown}{OP}=2100\cdot \pi \text{ km}.\\
~~[/tex]
Como os deslocamentos de [tex]N[/tex] a [tex]P[/tex] e de [tex]O[/tex] a [tex]N[/tex] são feitos sobre meridianos, temos que os comprimentos dos arcos [tex]\stackrel{\frown}{NO}[/tex] e [tex]\stackrel{\frown}{PN}[/tex] são iguais.
Note que o comprimento de [tex]\stackrel{\frown}{NO}[/tex] corresponde a um quarto de volta da circunferência terrestre. Logo,
[tex]\quad comp_\stackrel{\frown}{NO}=\dfrac{1}{4} \cdot 12600\cdot \pi \\
\quad comp_\stackrel{\frown}{NO}=3150\cdot \pi\text{ km}.\\
~~[/tex]
Como o comprimento [tex]T[/tex] do trajeto é a soma dos comprimentos dos arcos [tex]\stackrel{\frown}{NO}[/tex],[tex]\stackrel{\frown}{OP}[/tex] e [tex]\stackrel{\frown}{PN}[/tex], segue que
[tex]\qquad T=3150\cdot \pi +2100\cdot \pi + 3150\cdot \pi=8400\cdot \pi\text{ km},[/tex]
ou seja, aproximadamente, [tex]\boxed{26\,376\text{ km}}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Resumidamente, o caminho percorrido é o destacado em vermelho na imagem a seguir.
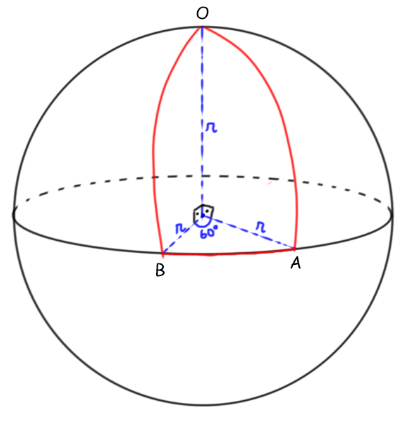
- As distâncias dos trajetos percorridos nas direções polo-meridiano e meridiano-polo são as mesmas e configuram um quarto do comprimento de uma circunferência de raio [tex]6300\text{ km}.[/tex] A soma dessas duas distâncias de mesma medida chamaremos de [tex]C_1[/tex] e é dada por:
[tex]\qquad C_1 = 2\cdot \left( \dfrac{2\cdot \pi \cdot 6300}{4}\right) \\
\qquad \boxed{C_1=19782\text{ km}}.[/tex] - Como o trajeto percorrido sobre a Linha do Equador define um ângulo central de [tex]60°[/tex], ele corresponde a um sexto de uma circunferência. Logo, a distância [tex]C_2[/tex] percorrida nesse trajeto pode ser assim calculada:
[tex]\qquad C_2 = \dfrac{2\cdot \pi \cdot 6300}{6} \\
\qquad \boxed{C_2 = 6594\text{ km}}.[/tex]
Portanto, o comprimento total [tex]C[/tex] percorrido nesse trajeto é dado, aproximadamente, por:
- [tex]C = C_1 + C_2 = 19782 + 6594 \\
~\fcolorbox{black}{#eee0e5}{$C=26\, 376\text{ km}$}\,.[/tex]
Solução elaborada pelo COM Phidias.
Nível B – Questão Mediana
