✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 1º ano do E. M.)
Com o roteiro abaixo, vamos construir uma prova geométrica para a desigualdade entre as médias aritmética e geométrica (MA e MG) de dois números positivos [tex]\,a\,[/tex] e [tex]\,b[/tex]. Vamos lá?
- Sobre uma reta suporte, construa dois círculos tangentes entre si. O de centro [tex]A[/tex] tem diâmetro com comprimento [tex]a[/tex] e, o de centro [tex]B[/tex], tem diâmetro com comprimento [tex]b[/tex], sendo [tex]a\geq b[/tex].
Qual é a medida do segmento [tex]\overline{AB}[/tex]? - Agora, considere um ponto [tex]C[/tex] no diâmetro com comprimento [tex]a[/tex] exibido, de tal forma que [tex]\overline{BC}[/tex] é perpendicular a [tex]\overline{AC}[/tex].
Qual é a medida de [tex]\overline{AC}[/tex]? - Quanto mede o segmento [tex]\overline{BC}[/tex]?
- Conclua a desigualdade MA-MG.
- Quando vale a igualdade?
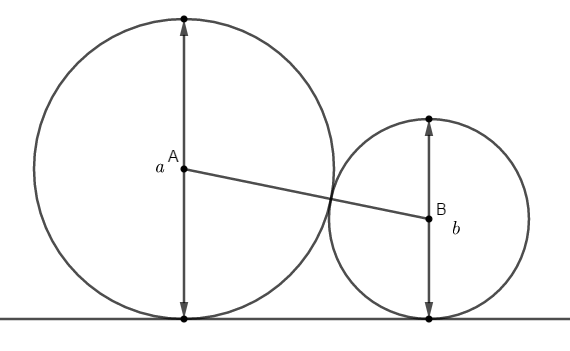
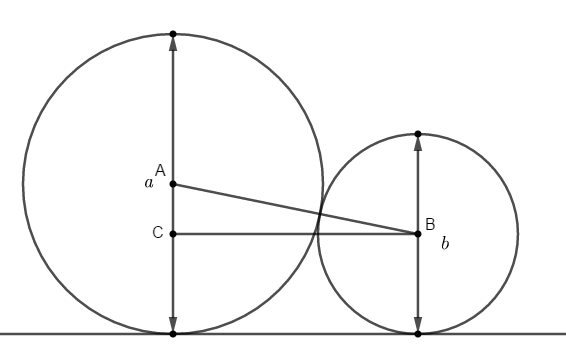
Adaptado de Proofs without Words: Exercises in Visual Thinking.

Lembretes
✏ Denominamos Média Aritmética dos números reais positivos [tex]\,a\,[/tex] e [tex]\,b[/tex] ao número denotado por [tex]MA[/tex] e assim definido: [tex]\boxed{MA=\dfrac{a+b}{2}}.[/tex]
✏ Denominamos Média Geométrica dos números reais positivos [tex]\,a\,[/tex] e [tex]\,b[/tex] ao número denotado por [tex]MG[/tex] e assim definido: [tex]\boxed{MG=\sqrt{a \cdot b\,}}.[/tex]
(Para conhecer um pouco mais sobre Médias e suas desigualdades, cliquem AQUI.)
Solução
Se [tex]\,a\,[/tex] e [tex]\,b[/tex] são números positivos, a partir da segunda imagem do enunciado, observamos que as medidas dos segmentos [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex] são a soma e a diferença entre os raios, respectivamente, ou seja, [tex]\dfrac{a+b}{2}[/tex] e [tex]\dfrac{a-b}{2}[/tex].
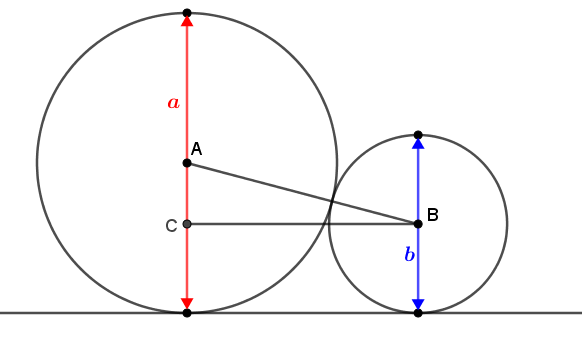
Assim, pelo Teorema de Pitágoras aplicado no triângulo retângulo [tex]ABC[/tex], temos:
[tex]\quad AB^{\,2}=AC^2+BC^2\\
\quad BC^2=AB^{\,2}-AC^2\\
\quad BC^2=\left(\dfrac{a+b}{2}\right)^2-\bigg(\dfrac{a-b}{2}\bigg)^2\\
\quad BC^2=\dfrac{a^2+2ab+b^2}{4}-\dfrac{a^2-2ab+b^2}{4}\\
\quad BC^2=\dfrac{4ab}{4}=ab\\
\quad \sqrt{BC^2}= \sqrt{ab}\\
\quad \left|BC\right|= \sqrt{ab~}. \qquad \textcolor{#800000}{(i)}[/tex]
Como [tex]BC[/tex] é a medida de um segmento, então [tex]BC \gt 0[/tex] e, portanto [tex]\left|BC\right|= BC.[/tex]
Com isso, segue de [tex]\textcolor{#800000}{(i)}[/tex] que [tex]BC=\sqrt{ab}\,.[/tex]
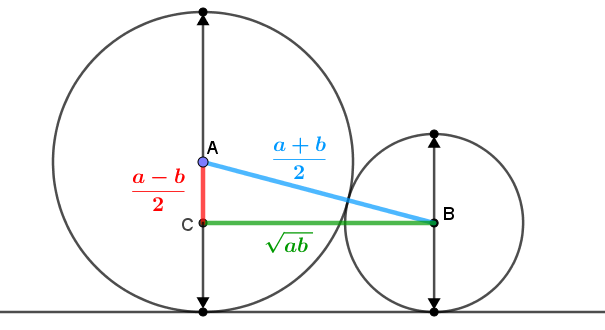
A conclusão da desigualdade decorre do fato de que, em um triângulo retângulo, a hipotenusa sempre é maior do que qualquer um dos catetos.
Então, [tex]AB\geq BC,[/tex] o que garante a desigualdade MA-MG:[tex]~\fcolorbox{#800000}{white}{$\dfrac{a+b}{2}\geq \sqrt{ab}$}\,.[/tex]
Para finalizar, perceba que a igualdade só pode ocorrer se o triângulo [tex]ABC[/tex] não existir, ou seja, se ele é degenerado num segmento, o que ocorre quando [tex]a=b[/tex] (neste caso, o ponto [tex]A[/tex] e o ponto [tex]C[/tex] coincidem).
Solução elaborada pelos Moderadores do Blog.
Para aprender mais…
Demonstração geométrica da desigualdade das médias
Vídeo extraído do Portal do Programa de Iniciação Cientifica da OBMEP
Professor Fabio Henrique Teixeira de Souza
