Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
Qual é o menor valor possível para [tex]A=|cos\,x|+|sen\,x|[/tex]?
Solução 1
Uma observação inicial:
- Como [tex]A[/tex] é não negativo, então [tex]A[/tex] vai ser mínimo quando [tex]A^2[/tex] for mínimo!
Veja que, elevando ao quadrado a expressão do enunciado, obtemos:
[tex]\qquad \qquad A^2=\left(|cos\,x|+|sen\,x|\right)^2[/tex]
[tex]\qquad \qquad A^2=\left(|cos\,x|\right)^2+2\cdot |cos\,x| \cdot|sen\,x|+\left(|sen\,x|\right)^2[/tex]
[tex]\qquad \qquad A^2=\left(cos\,x\right)^2+2\cdot |cos\,x| \cdot|sen\,x|+\left(sen\,x\right)^2[/tex]
[tex]\qquad \qquad A^2=cos^2x+2\cdot |cos\,x| \cdot|sen\,x|+sen^2x[/tex]
[tex]\qquad \qquad A^2=cos^2x+sen^2x+|2\cdot cos\,x \cdot sen\,x|. \qquad \textcolor{#800000}{(i)}[/tex]
Sabemos que [tex]\boxed{cos^2x+sen^2x=1}[/tex] e que [tex]\boxed{2\cdot cos\,x \cdot sen\,x=sen\,2x}[/tex]; assim, segue de [tex]\textcolor{#800000}{(i)}[/tex] que
[tex]\qquad \qquad A^2=\left(cos^2x+sen^2x\right)+|2\cdot cos\,x \cdot sen\,x|[/tex]
[tex]\qquad \qquad A^2=1+|sen\,2x|[/tex]
[tex]\qquad \qquad A^2-1=|sen\,2x|. \qquad \textcolor{#800000}{(ii)}[/tex]
Por outro lado, [tex]|sen\,2x| \geqslant 0[/tex]; logo, por [tex]\textcolor{#800000}{(ii)}[/tex], [tex]A^2-1 \geqslant 0[/tex], ou seja, [tex]A^2 \geqslant 1[/tex].
Portanto, o valor mínimo de [tex]A^2[/tex] é [tex]1[/tex], e, sendo [tex]A \gt 0[/tex], concluímos que o menor valor de [tex]A[/tex] é [tex]1.[/tex] (Esse valor pode ser obtido, por exemplo, com [tex]x=0[/tex]: [tex]A=|cos\,0|+|sen\,0|=1+0=1[/tex].)
Solução elaborada pelos Moderadores do Blog.
Solução 2
Considere o ciclo trigonométrico (círculo de raio unitário e centro na origem do plano cartesiano).
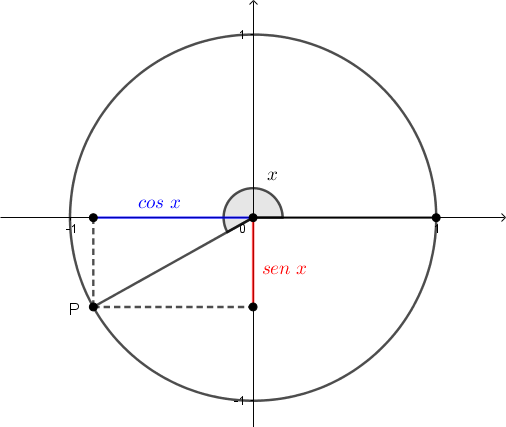
- Dado um valor real [tex]x[/tex], seja [tex]P[/tex] o ponto encontrado sobre o ciclo trigonométrico quando percorremos este círculo a partir do ponto [tex](1,0)[/tex] num comprimento [tex]x[/tex] (sentido anti-horário se [tex]x[/tex] é positivo e sentido horário se [tex]x[/tex] é negativo).
O ângulo central relativo ao arco percorrido será de [tex]x[/tex] radianos, o cosseno de [tex]x[/tex] será a abscissa do ponto [tex]P[/tex] e, o seno de [tex]x[/tex], sua ordenada: [tex]P=( cos \ x , sen\ x ).[/tex] - Observe então que os segmentos azul e vermelho da figura medem [tex]| cos \ x |, | sen\ x |[/tex], respectivamente, porque uma medida é sempre não negativa.
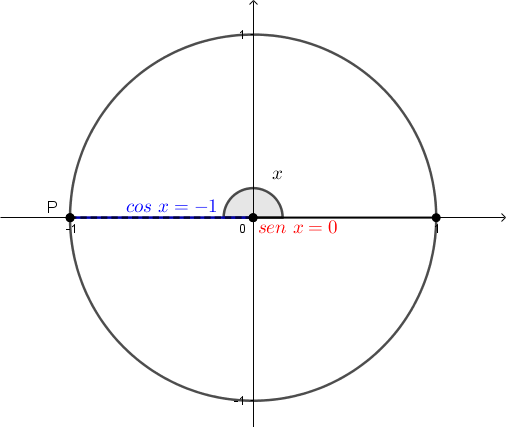
- Isto apenas não ocorre quando [tex]P[/tex] está sobre algum eixo. Para esses casos, temos [tex]|cos \ x|=1[/tex] e [tex]|sen\ x|=0[/tex] ou [tex]|sen \ x|=1[/tex] e [tex]|cos\ x|=0[/tex], o que nos dá [tex]A=1[/tex].
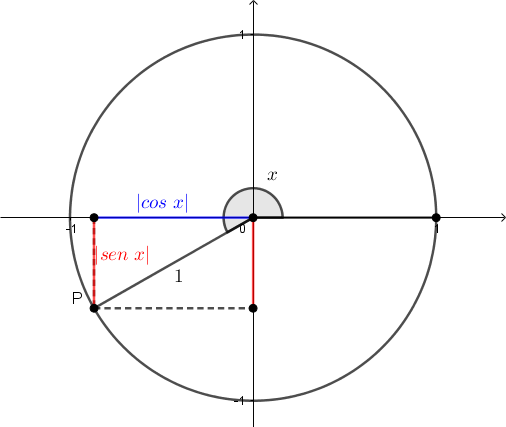
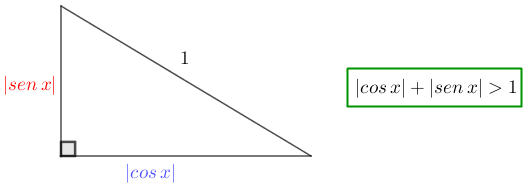
Assim, para a maior parte dos valores de [tex]x[/tex], temos um triângulo retângulo de catetos medindo [tex]| cos \ x |[/tex] e [tex]| sen\ x |[/tex] e hipotenusa medindo [tex]1[/tex]. Pela desigualdade triangular, temos [tex]1\lt |cos\,x|+|sen\,x|=A[/tex] nestes casos.
Portanto, o menor valor possível para [tex]A[/tex] é [tex]1[/tex].
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
