Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F.) (Nível: Fácil)
Caminhando [tex]100[/tex] metros pelo contorno de uma praça circular, uma pessoa descreve um arco de [tex]144^{\circ}[/tex].
Determinar a medida do raio da circunferência da praça.

Ajuda
A um arco de circunferência podemos associar duas medidas distintas:
✐ a sua medida angular;
✐ a sua medida linear.
Ambas podem ser obtidas a partir da medida angular e do comprimento da circunferência que define o arco; mas, se você não se lembra delas, clique AQUI.
Solução
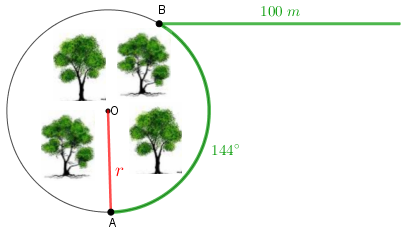
Pelos dados do problema, um arco de [tex]144^{\circ}[/tex] definido em uma circunferência de raio [tex]r[/tex] tem comprimento [tex]100[/tex] metros; assim podemos armar a seguinte regra de três simples:
| [tex]2\pi r[/tex] | ————————————– | [tex]360^\circ[/tex] |
| [tex]100 \,\, metros[/tex] | ————————————– | [tex]144^\circ[/tex] |
e obtemos que [tex]\boxed{2 \pi r \times 144=360 \times 100}[/tex].
Portanto:
[tex]\quad r=\dfrac{360 \times 100}{2\times \pi \times 144}[/tex]
[tex]\quad r=\dfrac{360 \times 50}{ \pi \times 144}[/tex]
[tex]\quad r=\dfrac{18000}{ \pi \times 144}[/tex]
[tex]\quad r=\dfrac{125}{ \pi}[/tex].
Dessa forma, o raio da praça é de aproximadamente [tex]39,8[/tex] metros.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
