Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M.) (Nível: Difícil)
Sejam [tex]a[/tex] e [tex]b[/tex] números reais distintos tais que [tex]a^2+b^2=6ab[/tex].
Determine o valor do quociente [tex]\dfrac{ a+b}{a-b}[/tex].

Para ajudar. . .
Vamos relembrar duas identidades que ajudam a simplificar expressões algébricas complicadas com as quais lidamos ao resolvermos alguns problemas. Em particular, elas praticamente resolvem este problema.
Para conhecer outras identidades algébricas que vocês podem utilizar na resolução de problemas, cliquem AQUI.
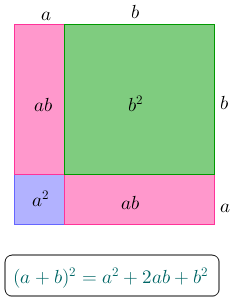
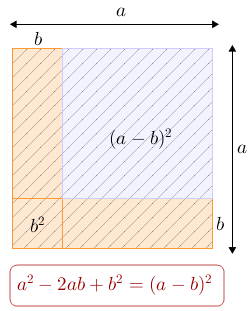
Se você não entendeu a interpretação geométrica, clicando no botão abaixo talvez você entenda.
1. Clique AQUI e espere o aplicativo carregar completamente.
2. Clique no ícone ► que irá aparecer no canto inferior esquerdo do aplicativo, para iniciar a animação.
3. Clique no ícone ▌▐ que apareceu no canto inferior esquerdo da janela, para parar a animação.
Solução
Sejam [tex]a \, [/tex] e [tex] \, b[/tex] dois números reais distintos que satisfazem a propriedade descrita no enunciado do problema:
[tex]\qquad \qquad \boxed{a^2+b^2=6ab}[/tex].[tex]\qquad \color{#800000}(i)[/tex]
Observe que como [tex]a^2+b^2 \gt 0[/tex], então [tex]ab \gt 0[/tex]; portanto [tex]a \, [/tex] e [tex] \, b[/tex] ou são ambos positivos ou são ambos negativos. (Note que ambos não podem ser iguais a zero, já que eles são distintos.)
De [tex]\color{#800000}(i)[/tex] segue que:
[tex]\qquad a^2+b^2+2ab=6ab+2ab[/tex]
[tex]\qquad a^2+2ab+b^2=8ab[/tex]
[tex]\qquad \left(a+b\right)^2=8ab.[/tex]
Como [tex]8ab \gt 0[/tex], podemos extrair a raiz quadrada de ambos os membros da última igualdade; com isso:
[tex]\qquad \sqrt{\left(a+b\right)^2}=\sqrt{8ab}[/tex]
[tex]\qquad |a+b|=\sqrt{8ab}[/tex]
[tex]\qquad a+b=\pm\sqrt{8ab}[/tex].[tex]\qquad \color{#800000}(ii)[/tex]
Utilizando, mais uma vez, a igualdade [tex]\color{#800000}(i)[/tex], segue que:
[tex]\qquad a^2+b^2-2ab=6ab-2ab[/tex]
[tex]\qquad a^2-2ab+b^2=4ab[/tex]
[tex]\qquad \left(a-b\right)^2=4ab.[/tex]
Como [tex]4ab \gt 0[/tex], podemos, também, extrair a raiz quadrada de ambos os membros da última igualdade e com isso:
[tex]\qquad \sqrt{\left(a-b\right)^2}=\sqrt{4ab}[/tex]
[tex]\qquad |a-b|=\sqrt{4ab}[/tex]
[tex]\qquad a-b=\pm\sqrt{4ab}[/tex].[tex]\qquad \color{#800000}(iii)[/tex]
Pronto, como [tex]ab\ne0[/tex], por [tex]\color{#800000}(ii)[/tex] e [tex]\color{#800000}(iii)[/tex] temos que:
[tex]\qquad \dfrac{ a+b}{a-b}=\dfrac{\pm\sqrt{8ab}}{\pm\sqrt{4ab}}[/tex]
[tex]\qquad \dfrac{ a+b}{a-b}=\pm\sqrt{\dfrac{8ab}{4ab}}[/tex]
[tex]\qquad \dfrac{ a+b}{a-b}=\pm\sqrt{2}[/tex]
Portanto, temos dois valores possíveis para o quociente em questão: [tex]\quad \fcolorbox{black}{#FFEFD5}{$\dfrac{ a+b}{a-b}=\sqrt{2}$}\quad [/tex] ou [tex]\quad \fcolorbox{black}{#E6E6FA}{$\dfrac{ a+b}{a-b}=-\sqrt{2}$}[/tex] .
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
