Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
Um balão está preso ao solo por dois cabos de aço em dois pontos que se distanciam entre si de [tex]60[/tex] metros. Os dois cabos estão completamente esticados, sendo que o cabo mais curto mede [tex]80\text{ m}[/tex] e o ângulo que o outro cabo faz com o solo mede [tex]30^\circ.[/tex]
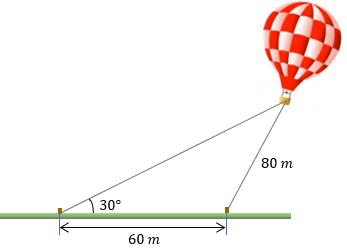Imagem do balão extraída de Freepik
(a) Qual o comprimento do cabo mais longo?
(b) No momento descrito pelos dados, a que altura o balão está do solo?
Ajuda
✐ Definição: Seja [tex]ACB[/tex] um triângulo retângulo com catetos e hipotenusa com comprimentos [tex]a,\, b,\, h[/tex], respectivamente. Seja [tex]\theta[/tex] a medida em graus de um dos ângulos agudos desse triângulo, [tex]0^{\circ} \lt\theta\lt 90^{\circ}[/tex].
Chamamos de tangente de [tex]\theta[/tex], e denotamos por [tex]tg\, \theta[/tex], a razão entre os comprimentos dos catetos oposto e adjacente a [tex]\theta[/tex]: [tex]\boxed{ tg\, \theta= \dfrac{a}{b}}.[/tex]
✐ No estudo da trigonometria, alguns ângulos são bastante utilizados e devido à frequência com que eles surgem em problemas e à importância que eles têm para a Geometria são denominados ângulos notáveis ou ângulos especiais ou, ainda, ângulos fundamentais. São eles os ângulos com medidas iguais a: [tex]30^\circ[/tex], [tex] 45^{\circ} [/tex] e [tex]60^\circ[/tex]. As tangentes desses ângulos são:
[tex] \qquad \qquad tg\, 30^{\circ}=\dfrac{\sqrt{3}}{3}\quad ; \quad tg\, 45^{\circ}=1\quad ;\quad tg\, 60^{\circ}=\sqrt{3}[/tex].
✐ Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
Solução
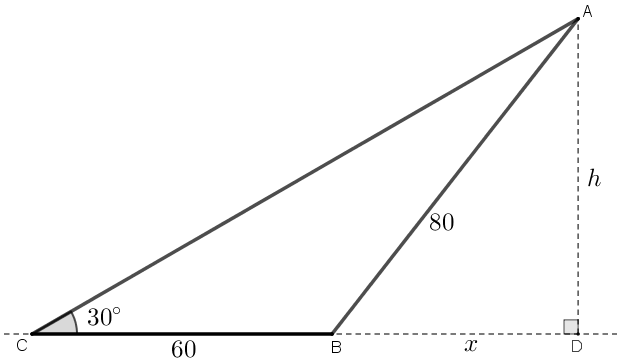
A partir dos dados do problema, definimos o triângulo [tex]ABC\,[/tex] e traçamos o segmento [tex]AD[/tex], ortogonal ao segmento [tex]CB[/tex], conforme mostra a figura a seguir.
Denotamos por [tex]h\,[/tex] o comprimento em metros do segmento [tex]AD[/tex] – altura em que se encontra o balão – e por [tex]x\,[/tex] o comprimento em metros do segmento [tex]BD[/tex] – distância entre o pé da perpendicular e o ponto do solo no qual está preso o cabo mais curto.
Aplicando o Teorema de Pitágoras ao triângulo retângulo [tex]ABD[/tex], obtemos que
[tex]\qquad x^2+h^2=80^2.\qquad \textcolor{#800000}{(i)}[/tex]
Por outro lado, olhando o triângulo [tex]ADC[/tex], observamos que [tex]tg\,30^\circ=\dfrac{h}{60+x}[/tex] e, portanto, segue que:
[tex]\qquad \dfrac{\sqrt{3}}{3}=\dfrac{h}{60+x}\\
\qquad h=\left(60+x\right)\cdot \dfrac{\sqrt{3}}{3}.\qquad \textcolor{#800000}{(ii)}[/tex]
Dessa forma, substituindo [tex]\textcolor{#800000}{(ii)}[/tex] em [tex]\textcolor{#800000}{(i)}[/tex] segue que:
[tex]\qquad x^2+\left(\left(60+x\right)\cdot \dfrac{\sqrt{3}}{3}\right)^2=80^2\\
\qquad x^2+\left(60+x\right)^2\cdot \dfrac{3}{9}=6400 \\
\qquad x^2+\left(3600+120x+x^2\right)\cdot \dfrac{1}{3}=6400 \\
\qquad 3x^2+\left(3600+120x+x^2\right)=3\cdot 6400 \\
\qquad 4x^2+3600+120x=19200 \\
\qquad 4x^2+120x-15600=0.[/tex]
Dividindo a última igualdade por [tex]4[/tex] ficamos com a equação [tex]\boxed{x^2+30x-3900=0}[/tex] cujas raízes são dadas por:
[tex]\qquad x=\dfrac{-30\pm\sqrt{900+15600}}{2}\\
\qquad x=\dfrac{-30\pm\sqrt{16500}}{2}\\
\qquad x_1=\dfrac{-30+\sqrt{16500}}{2} \;\text{ e } \; x_2=\dfrac{-30-\sqrt{16500}}{2}.\\[/tex]
Vemos que [tex]x_2 \lt 0[/tex]; logo, essa raiz não pode ser solução do problema, já que estamos procurando um comprimento e, portanto, um valor positivo.
Então,
[tex]\qquad x=\dfrac{-30+\sqrt{16500}}{2}\approx 49,23\text{ m}[/tex]
e, consequentemente, por [tex]\textcolor{#800000}{(ii)}[/tex]:
[tex]\qquad h=\left(60+x\right)\cdot \dfrac{\sqrt{3}}{3}\\
\qquad h\approx\left(60+ 49,23\right)\cdot \dfrac{\sqrt{3}}{3}\\
\qquad h\approx\left(109,23\right)\cdot \dfrac{\sqrt{3}}{3}\\
\qquad h\approx 63,06\text{ m}.[/tex]
A partir do triângulo [tex]ADC[/tex], mostrado na figura a seguir com as medidas que acabamos de calcular, já temos condições de responder os dois itens do problema.
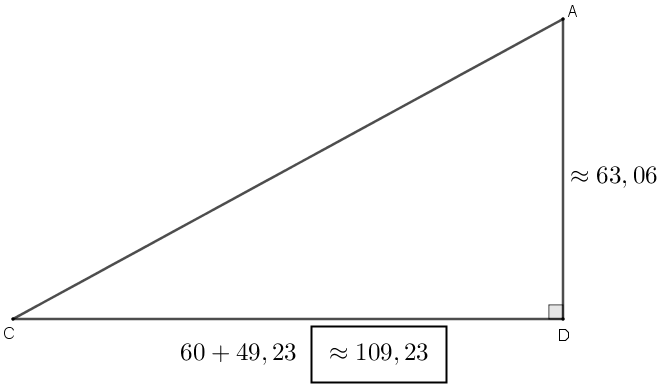
(a) Para calcularmos o comprimento do cabo mais longo, vamos aplicar o Teorema de Pitágoras ao triângulo [tex]ADC[/tex], lembrando que estamos trabalhando com medidas aproximadas.
Assim, se [tex]z[/tex] é a medida em metros do cabo mais longo, então o comprimento do segmento [tex]AC[/tex] é [tex]z[/tex] e, com isso:
[tex]\qquad z^2\approx 109,23^2+63,06^2\\
\qquad z^2\approx 15907,76\\
\qquad z\approx 126,13\,.[/tex]
Pelo exposto, o comprimento do cabo mais longo é aproximadamente [tex]\fcolorbox{black}{#eee0e5}{$126,13 \text{ m}$}\,.[/tex]
(b) Observamos diretamente na figura acima que, no momento descrito pelos dados, o balão está a uma altura do solo de aproximadamente [tex]\fcolorbox{black}{#eee0e5}{$63,06 \text{ m}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
|
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |