Problema
(Indicado a partir do 2º ano do E. M.)
No jogo de xadrez, a Defesa Francesa ocorre quando o jogador das peças pretas responde ao lance inicial 1. e4 das brancas (avanço do peão em frente do rei branco duas casas) com o lance 1… e6 (avanço do peão em frente do rei preto uma casa).
Por meio de consultas a bancos de dados é possível saber que um jogador aleatório tem uma probabilidade próxima a [tex]1/8[/tex] de empregar a Defesa Francesa contra o lance inicial 1. e4 das brancas.
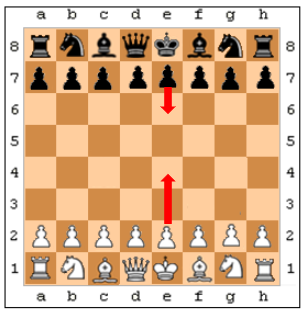

Defesa Francesa.
Se um jogador sempre inicia suas partidas com 1. e4, qual é a probabilidade de ele enfrentar a Defesa Francesa pelo menos uma vez nos próximos [tex]5[/tex] jogos, assumindo-se que seus oponentes se comportem de forma independente?

AJUDA
✐ Sabemos que um evento [tex]E[/tex] pode ocorrer ou não. Se o evento [tex]E[/tex] for relativo a um espaço amostral [tex]\, \Omega[/tex], o evento associado à não ocorrência de [tex]E[/tex] é denominado o complementar de [tex]E[/tex] com relação a [tex]\, \Omega[/tex] e é denotado por [tex]\overline{E}[/tex].
- Logo, [tex]\overline{E}[/tex] ocorre se, e somente se, [tex]E[/tex] não ocorrer.
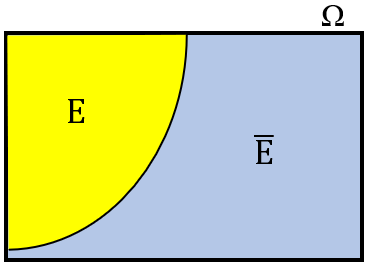
Dessa forma, se [tex]P[/tex] for a probabilidade de que o evento [tex]E[/tex] ocorra (sucesso) e [tex]Q[/tex] for a probabilidade de que [tex]E[/tex] não ocorra (insucesso), então [tex]Q[/tex] é a probabilidade do evento complementar [tex]\overline{E}[/tex], ou simplesmente probabilidade complementar de [tex]P[/tex], e temos a seguinte relação: [tex]\boxed{P+Q=1}\, .[/tex]
✐ Princípio Fundamental da Contagem, ou Princípio Multiplicativo, para [tex]k [/tex] decisões : Se
- uma decisão D1 puder ser tomada de [tex] m_1 [/tex] maneiras distintas,
- uma decisão D2 puder ser tomada de [tex] m_2 [/tex] maneiras distintas,
- [tex]\cdots[/tex]
- uma decisão Dk puder ser tomada de [tex]m_k [/tex] maneiras distintas e
- todas essas decisões forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha de outra),
então o número total de maneiras de tomarmos sucessivamente essas [tex]k[/tex] decisões é igual ao produto
[tex]\qquad \qquad \boxed{m_1\times m_2 \times \cdots \times m_k} \, .[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
Solução
A probabilidade de um jogador não enfrentar a Defesa Francesa contra um oponente aleatório é de [tex]1-1/8=7/8[/tex].
Assim, considerando que os jogadores se comportem de forma independente, pelo Princípio Fundamental da Contagem, a probabilidade de um jogador que sempre inicia suas partidas com 1. e4 não enfrentar a Defesa Francesa nos seus próximos [tex]5[/tex] jogos é de [tex]\left(\frac{7}{8}\right)^5[/tex]. Logo, a probabilidade complementar [tex]p[/tex] de ele se deparar com a Defesa Francesa pelo menos uma vez é dada por:
[tex]\qquad \fcolorbox{black}{#eee0e5}{$p=1-\left(\frac{7}{8}\right)^5\approx 0,487$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
