✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F.- Nível de dificuldade: Difícil)
Agora, vamos fazer a diferença entre o maior e o menor desses dois números e, em seguida, vamos somar essa diferença com o número que obtemos invertendo a ordem de seus dígitos.
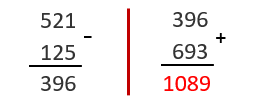
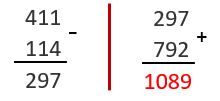
Isso foi uma coincidência ou o procedimento apresentado resulta sempre em [tex]1089[/tex], independentemente do número de três dígitos que seja utilizado?
Solução
No problema, temos que verificar se o procedimento apresentado resulta SEMPRE em [tex]1089[/tex], INDEPENDENTEMENTE do número de três dígitos que seja utilizado.
As duas palavras destacadas, SEMPRE e INDEPENDENTEMENTE, indicam que devemos fazer uma análise genérica tomando por base um número [tex]n[/tex] de três algarismos.
Seja, então, [tex]n=abc[/tex] o número dado e [tex]m=cba[/tex] o que obtemos invertendo a ordem dos algarismos de [tex]n[/tex].
(Antes de prosseguir, observe que aqui as notações [tex]abc[/tex] e [tex]cba[/tex] não indicam produtos e sim a representação dos números de três algarismos [tex]n[/tex] e [tex]m[/tex] no sistema decimal.)
Ao fazermos a diferença entre o maior e o menor desses dois números, estamos implicitamente supondo que eles são distintos (até porque, se eles forem iguais, a diferença entre eles seria zero e a propriedade em questão não seria verificada); portanto, suponha, sem perda de generalidade, que [tex]n \gt m[/tex]. Neste caso, como [tex]abc \gt cba[/tex], perceba que [tex]a \gt c[/tex], já que [tex]a \lt c[/tex] implica em [tex]m \lt n[/tex] e [tex]a = c[/tex] implica em [tex]m=n[/tex] [tex](n=aba=cbc=m)\,.[/tex]
Dessa forma, ao fazermos o esqueminha da subtração, colocando os números de forma que tenhamos os algarismos da centena, dezena e unidade do menor embaixo dos algarismos da centena, dezena e unidade do maior, respectivamente, teremos um probleminha para começar a fazer a subtração.
[tex]\begin{array}{c c c }
\textcolor{#FF00FF}{Ce}&\textcolor{#3BB9FF}{De}&\textcolor{red}{Un}\\
\,a&b&c\,\\
\,c&b&a\,\\
\hline
\end{array}\,-[/tex]
Percebeu?
Como [tex]c \lt a[/tex], não podemos tirar [tex]a[/tex] unidades de [tex]c[/tex]. Então, o jeito é emprestar uma unidade de dezena do [tex]b[/tex] para o [tex]c[/tex] no minuendo da subtração (lembre-se de que [tex]\textcolor{#3BB9FF}{1}[/tex] dezena corresponde a [tex]\textcolor{red}{10}[/tex] unidades):
[tex]\begin{array}{c|c|c}
\textcolor{#FF00FF}{Ce}&\textcolor{#3BB9FF}{De}&\textcolor{red}{Un}\\
\,&b-\textcolor{#3BB9FF}{1}&c+\textcolor{red}{10}\,\\
\,a&\cancel{b}&\cancel{c}\,\\
\,c&b&a\,\\
\hline
\end{array}\,[/tex][tex]\begin{array}{l}
\\
\\
-\\
\\
\end{array}[/tex]
e fazer esta subtração:
[tex]\begin{array}{c|c|c}
\textcolor{#FF00FF}{Ce}&\textcolor{#3BB9FF}{De}&\textcolor{red}{Un}\\
a\,&b-\textcolor{#3BB9FF}{1}&c+\textcolor{red}{10}\,\\
\,c&b&a\,\\
\hline
\end{array}\,-[/tex]
Pronto, feita a diferença relativa à coluna das unidades, ficamos com outro probleminha: na coluna das dezenas, não conseguimos tirar [tex]b[/tex] unidades de [tex]b-1[/tex] unidades.
[tex]\begin{array}{c|c|c}
\textcolor{#FF00FF}{Ce}&\textcolor{#3BB9FF}{De}&\textcolor{red}{Un}\\
a\,&b-\textcolor{#3BB9FF}{1}&c+\textcolor{red}{10}\,\\
\,c&b&a\,\\
\hline
\,&&(c+10)-a\,\end{array}\,-[/tex]
Agora, o jeito é emprestar uma unidade de centena do [tex]a[/tex] para o [tex]b-1[/tex] no minuendo da subtração; e lembre-se de que [tex]\textcolor{#FF00FF}{1}[/tex] centena corresponde a [tex]\textcolor{#3BB9FF}{10}[/tex] dezenas:
[tex]\begin{array}{c|c|c}
\textcolor{#FF00FF}{Ce}&\textcolor{#3BB9FF}{De}&\textcolor{red}{Un}\\
\,&(b-\textcolor{#3BB9FF}{1})+\textcolor{#3BB9FF}{10}&\,\\
\,a-\textcolor{#FF00FF}{1}&\cancel{b-\textcolor{#3BB9FF}{1}}&c+\textcolor{red}{10}\,\\
\,c&b&a\,\\
\hline
\,&&(c+10)-a\,\end{array}\,-[/tex]
e fazer a diferença relativa à coluna das dezenas.
[tex]\begin{array}{c|c|c}
\textcolor{#FF00FF}{Ce}&\textcolor{#3BB9FF}{De}&\textcolor{red}{Un}\\
\,a-\textcolor{#FF00FF}{1}&(b-\textcolor{#3BB9FF}{1})+\textcolor{#3BB9FF}{10}&c+\textcolor{red}{10}\,\\
\,c&b&a\,\\
\hline
\,&9&(c+10)-a\,\end{array}\,-[/tex]
Já podemos, então, finalizar a nossa subtração.
[tex]\begin{array}{c|c|c}
\textcolor{#FF00FF}{Ce}&\textcolor{#3BB9FF}{De}&\textcolor{red}{Un}\\
\,a-\textcolor{#FF00FF}{1}&(b-\textcolor{#3BB9FF}{1})+\textcolor{#3BB9FF}{10}&c+\textcolor{red}{10}\,\\
\,c&b&a\,\\
\hline
\,(a-1)-c&9&(c+10)-a\,\end{array}\,-[/tex]
Finalmente, vamos somar a diferença obtida com o número resultante da inversão dos algarismos dessa diferença, observe:
[tex]\begin{array}{c|c|c}
\textcolor{#FF00FF}{Ce}&\textcolor{#3BB9FF}{De}&\textcolor{red}{Un}\\
\textcolor{#FF00FF}{1}&&\\
\,(a-1)-c&9&(c+10)-a\,\\
\,(c+10)-a&9&\,(a-1)-c\,\\
\hline
\,1-1+10&8&\,10-1\,\\
\end{array}\,\;\;+[/tex]
ou seja
[tex]\begin{array}{c|c|c}
\textcolor{#52D017}{Mi}&\textcolor{#FF00FF}{Ce}&\textcolor{#3BB9FF}{De}&\textcolor{red}{Un}\\
\textcolor{#52D017}{1}&&\\
&\,(a-1)-c&9&(c+10)-a\,\\
&\,(c+10)-a&9&\,a-1-c\,\\
\hline
1&\,0&8&9\,\\
\end{array}\,\;\;+[/tex]
Portanto, não foi uma coincidência termos obtido [tex]1089[/tex] aplicando o procedimento proposto nos dois exemplos apresentados.
Apenas uma observação: o número inicialmente escolhido deve ter os algarismos da unidade e da centena distintos, para que o número obtido com a inversão dos algarismos seja distinto do original.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
