✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 1º ano do E. M. – Nível de dificuldade: Médio)
Determine todos os valores reais de [tex]~x~[/tex] tais que [tex]\dfrac{2x+1}{x+2} \lt 5\,.[/tex]

Ajuda
✐ A nossa ajuda para este problema se resume a uma única observação:
Quando lidamos com igualdades, podemos fazer uma mesma operação em ambos os membros sem muita preocupação. Contudo, vale lembrar que:
- Ao multiplicarmos ambos os membros de uma desigualdade por um número negativo, é necessário inverter o sinal da desigualdade.
Solução 1
Em função da observação feita acima, podemos considerar as duas situações possíveis em termos de sinal do denominador [tex]x+2[/tex]:
- [tex]x+2 \gt 0[/tex]
- [tex]x+2 \lt 0[/tex]
e resolver as duas desigualdades resultantes, não esquecendo de levar em conta em cada solução os valores que fazem com que o denominador seja positivo ou negativo.
A solução final será a união das duas soluções obtidas. Então, vamos lá!
[tex]\textcolor{#800000}{(1)}[/tex] Suponhamos, inicialmente, que [tex]x+2 \gt 0[/tex]. Assim, nesta discussão estaremos trabalhando com valores de [tex]x[/tex] tais que
[tex]\qquad \qquad x \gt -2. \qquad \textcolor{#800000}{(i)}[/tex]
Como estamos considerando [tex]x+2 \gt 0[/tex], podemos multiplicar a desigualdade [tex]\dfrac{2x+1}{x+2} \lt 5[/tex] por [tex]x+2 [/tex] sem alterar o sinal de desigualdade. Assim, temos a seguinte sequência de desigualdades equivalentes:
[tex]\qquad \dfrac{2x+1}{x+2} \lt 5\\
\qquad 2x+1 \lt 5\cdot\left(x+2\right)\\
\qquad 2x+1 \lt 5x+10\\
\qquad 2x-5x \lt 10-1\\
\qquad -3x \lt 9\\
\qquad 3x \gt -9\\
\qquad x \gt\dfrac{-9}{3}\\
\qquad x \gt-3. \qquad \textcolor{#800000}{(ii)}[/tex]
Temos, então, duas restrições para os valores de [tex]x[/tex] que devem ser simultaneamente satisfeitas: condição [tex]\textcolor{#800000}{(i)}[/tex] e condição [tex]\textcolor{#800000}{(ii)}\,.[/tex]
► Observe que a condição [tex]\textcolor{#800000}{(i)}[/tex] é satisfeita pelos elementos do intervalo aberto [tex]]-2\,,+\infty[[/tex] e a condição [tex]\textcolor{#800000}{(ii)}[/tex] é satisfeita pelos elementos do intervalo [tex]]-3\,,+\infty[[/tex]; logo, ambas condições são satisfeitas pela interseção desses dois intervalos, ou seja, pelo próprio intervalo [tex]\,]-2\,,+\infty[\,[/tex], já que [tex]\, ]-2\,,+\infty[\,\, \subset\,\,]-3\,,+\infty[\,.[/tex]
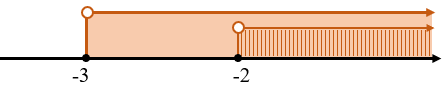
O intervalo [tex]\,]-2\,,+\infty[\,[/tex] é, então, a primeira parte da solução.
[tex]\textcolor{#800000}{(2)}[/tex] Suponhamos, agora, que [tex]x+2 \lt 0[/tex]. Assim, nesta discussão estaremos trabalhando com valores de [tex]x[/tex] tais que
[tex]\qquad \qquad x \lt -2. \qquad \textcolor{#800000}{(iii)}[/tex]
Como estamos considerando [tex]x+2 \lt 0[/tex], ao multiplicarmos a desigualdade [tex]\dfrac{2x+1}{x+2} \lt 5[/tex] por [tex]x+2 [/tex] devemos alterar o sinal de desigualdade. Desta vez, temos a seguinte sequência de desigualdades equivalentes:
[tex]\qquad \dfrac{2x+1}{x+2} \lt 5\\
\qquad 2x+1 \textcolor{red}{\gt} 5\cdot\left(x+2\right)\\
\qquad 2x+1 \gt 5x+10\\
\qquad 2x-5x \gt 10-1\\
\qquad -3x \gt 9\\
\qquad 3x \lt -9\\
\qquad x \lt\dfrac{-9}{3}\\
\qquad x \lt-3. \qquad \textcolor{#800000}{(iv)}[/tex]
Temos, agora, duas restrições para os valores de [tex]x[/tex] que devem ser simultaneamente satisfeitas: condição [tex]\textcolor{#800000}{(iii)}[/tex] e condição [tex]\textcolor{#800000}{(iv)}\,.[/tex]
► Note que a condição [tex]\textcolor{#800000}{(iii)}[/tex] é satisfeita pelos elementos do intervalo aberto [tex]]-\infty\, , \, -2[[/tex] e a condição [tex]\textcolor{#800000}{(iv)}[/tex] é satisfeita pelos elementos do intervalo [tex]]-\infty\, , \, -3[[/tex]; logo, ambas condições são satisfeitas pela interseção desses dois intervalos, ou seja, pelo próprio intervalo [tex]\,]-\infty\, , \, -3[\,[/tex], uma vez que [tex]\, ]-\infty\, , \, -3[\,\, \subset\,\,]-\infty\, , \, -2[\,.[/tex]

O intervalo [tex]\,]-\infty\, , \, -3[\,[/tex] é a segunda parte da solução.
Finalmente, por [tex]\textcolor{#800000}{(1)}[/tex] e por [tex]\textcolor{#800000}{(2)}[/tex], concluímos que os valores reais de [tex]~x~[/tex] tais que [tex]\dfrac{2x+1}{x+2} \lt 5\,[/tex] são de dois tipos:
- os números reais maiores do que [tex]-2[/tex] e também os números reais menores do que [tex]-3[/tex],
ou seja, os valores de [tex]x[/tex] que pertencem à união [tex]\,\fcolorbox{black}{#ffd3d3}{$]-\infty\, , \, -3[\, \cup \,]-2\,,+\infty[$}\,.[/tex]
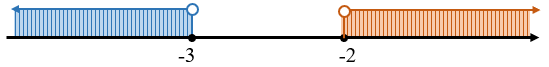
Solução elaborada pelos Moderadores do Blog.
Solução 2
Poderíamos ter evitado a divisão da análise de sinal do denominador resolvendo a desigualdade proposta sem multiplicá-la por [tex]x+2.[/tex]
Vejamos como!
Observe a seguinte sequência de desigualdades equivalentes:
\begin{equation}\boxed{\dfrac{2x+1}{x+2} \lt 5} \iff \dfrac{2x+1}{x+2}-5\lt 0 \iff \dfrac{2x+1-5\cdot (x+2)}{x+2}\lt 0 \iff \\
\quad \iff \dfrac{2x+1-5x-10}{x+2}\lt 0 \iff \boxed{\dfrac{-3x-9}{x+2}\lt 0}\,.\end{equation}
Como [tex]\dfrac{2x+1}{x+2} \lt 5 \iff \dfrac{-3x-9}{x+2}\lt 0[/tex], podemos resolver a desigualdade [tex]\ \dfrac{-3x-9}{x+2}\lt 0[/tex] para resolver o problema. E para resolver essa desigualdade, faremos isoladamente a análise de sinal das expressões [tex]-3x-9[/tex] e [tex]x+2[/tex] e, a partir dessas análises, analisaremos o sinal da expressão [tex]\dfrac{-3x-9}{x+2}[/tex] em função da variação de [tex]x[/tex].
Vejamos.
[tex]\textcolor{#800000}{(1)}[/tex] Análises isoladas de sinal
Analisar o sinal de uma expressão significa saber para que valores de [tex]x[/tex] a expressão define um número positivo, um número negativo ou o número [tex]0[/tex]. E não precisa adivinhar, é só fazer continhas…
|
[tex]\quad x+2 \gt 0 \iff x\gt -2 [/tex] [tex]\quad x+2 \lt 0 \iff x\lt -2 [/tex] [tex]\quad x+2 = 0 \iff x = -2 [/tex] |
[tex]\quad -3x-9 \lt 0 \iff -3x\lt 9 \iff x\gt -3 [/tex] [tex]\quad -3x-9 \gt 0 \iff -3x\gt 9 \iff x\lt -3[/tex] [tex]\quad -3x-9 = 0 \iff -3x= 9 \iff x= -3 [/tex] |
[tex]\textcolor{#800000}{(2)}[/tex] Análise de sinal da expressão [tex]\dfrac{-3x-9}{x+2}[/tex].
Vamos representar as análises de sinal do item anterior, considerando a reta real. Para isso, observamos que:
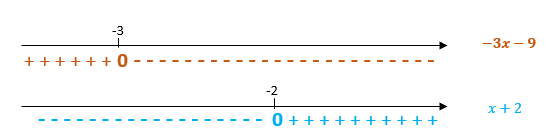
- a análise do sinal de [tex]-3x-9[/tex] nos diz que à direita de [tex]-3[/tex] a expressão é negativa; à esquerda de [tex]-3[/tex] a expressão é positiva e para [tex]x=-3[/tex] a expressão é zero.
- a análise do sinal de [tex]x+2[/tex] nos diz que à direita de [tex]-2[/tex] a expressão é positiva ; à esquerda de [tex]-2[/tex] a expressão é negativa e para [tex]x=-2[/tex] a expressão é zero.
Esquematicamente:
Lembrando das regrinhas de sinal para produtos e divisões:
- produto/quociente de números com sinais contrários é um número negativo;
- produto/quociente de números com mesmo sinal é um número positivo;
podemos, finalmente, obter a variação de sinal da expressão [tex]\dfrac{-3x-9}{x+2}[/tex].
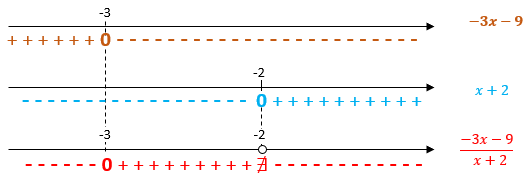
Como [tex]\,\dfrac{2x+1}{x+2} \lt 5 \,\,[/tex] e [tex] \,\,\dfrac{-3x-9}{x+2}\lt 0\,[/tex] são desigualdades equivalentes, então a solução da desigualdade [tex]\dfrac{2x+1}{x+2} \lt 5 [/tex] são os valores de [tex]x[/tex] para os quais a expressão [tex]\dfrac{-3x-9}{x+2}[/tex] é negativa.
Assim, olhando a variação de sinal da expressão [tex]\dfrac{-3x-9}{x+2}[/tex], vemos que devemos ter [tex]\,\fcolorbox{black}{#ffd3d3}{$ x\lt -3 \text{ ou } x \gt -2$}\,[/tex] para que a desigualdade [tex]\,\boxed{\dfrac{2x+1}{x+2} \lt 5} \,[/tex] seja satisfeita. Esses valores correspondem à união [tex]\,\fcolorbox{black}{#ffd3d3}{$]-\infty\, , \, -3[\, \cup \,]-2\,,+\infty[$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
