Problema
(Indicado a partir do 9º ano do E. F.)
Considere o trapézio [tex]ABCD[/tex] cujas bases [tex]\overline{AB}[/tex] e [tex]\overline{CD}[/tex] medem [tex]5\;cm[/tex] e [tex]3\;cm[/tex], respectivamente. As diagonais [tex]\overline{AC}[/tex] e [tex]\overline{BD}[/tex] interceptam-se no ponto [tex]O[/tex]. Calcule a razão entre as áreas do triângulo [tex]ABO[/tex] e do trapézio [tex]ABCD[/tex].
Solução
Notações:
(1) Vamos denotar o triângulo formado pelos vértices, digamos, [tex]X, Y[/tex] e [tex]Z[/tex] por [tex]\Delta XYZ[/tex] e sua área por [tex]A(\Delta XYZ)[/tex].
(2) A área do trapézio [tex]ABCD[/tex] denotaremos por [tex]A(ABCD)[/tex].
(3) O segmento definidos pelos pontos, digamos, [tex]X[/tex] e [tex]Y[/tex] será denotado por [tex]\overline{XY}[/tex] e, seu comprimento, por [tex]XY[/tex].
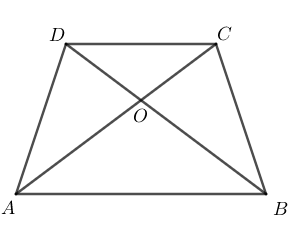
Observe que os pares de ângulos "[tex]B\hat D C[/tex] e [tex]D\hat BA[/tex]" e "[tex]D\hat CA[/tex] e [tex]C\hat AB[/tex]" são alternos internos e, portanto, os ângulos de cada par têm a mesma medida. (Precisa relembrar esse conceito? Dê uma passadinha nesta Sala.)
Dessa forma, pelo caso de semelhança de triângulos A.A. (ângulo – ângulo) (Para recordar casos de semelhança de triângulos, visite esta Sala) temos que [tex]\Delta AOB[/tex] e [tex]\Delta COD[/tex] são semelhantes.
Assim,
[tex]\qquad \qquad \dfrac{CO}{AO}=\dfrac{DO}{BO}=\dfrac{CD}{AB}=\dfrac{3}{5}.\;\;\;\;\; [/tex]
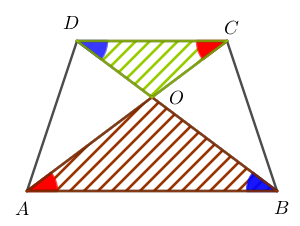
E como a razão entre as áreas de dois triângulos semelhantes é dada pelo quadrado da razão de semelhança entre eles, temos que
[tex]\qquad \qquad \dfrac{A(\Delta COD)}{A(\Delta AOB)}=\bigg(\dfrac{3}{5}\bigg)^2.\;\;\;\;\; \textcolor{#800000}{(i)}[/tex]
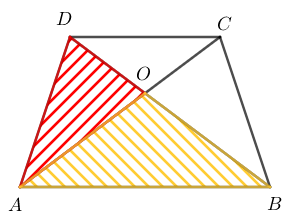
Notemos que [tex]\Delta AOB[/tex] e [tex]\Delta AOD[/tex] possuem a mesma altura em relação às suas bases [tex]\overline{OB}[/tex] e [tex]\overline{OD}[/tex], respectivamente. Logo, suas áreas são proporcionais às suas bases. Pela semelhança de [tex]\Delta AOB[/tex] e [tex]\Delta COD[/tex] tem-se:
[tex]\qquad \qquad \dfrac{A(\Delta AOD)}{A(\Delta AOB)}=\dfrac{OD}{OB}=\dfrac{3}{5}.\;\;\;\;\; \textcolor{#800000}{(ii)}[/tex]
Vamos observar os triângulos [tex]\Delta ADC[/tex] e [tex]\Delta BCD[/tex].
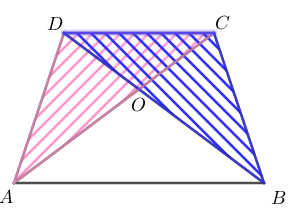
Eles possuem a mesma base [tex]\overline{CD}[/tex] e a mesma altura (altura do trapézio). Assim, [tex]A(\Delta ADC)=A(\Delta BCD).[/tex]
Da mesma maneira, [tex]A(\Delta ABD)=A(\Delta ABC).[/tex]
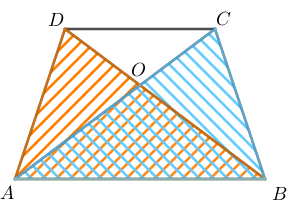
Observe agora que:
[tex]\qquad \qquad A(\Delta ABD)=A(\Delta AOB)+A(\Delta AOD)[/tex]
e
[tex]\qquad \qquad A(\Delta ABC)=A(\Delta AOB)+A(\Delta BCO)[/tex];
logo,
[tex]\qquad \qquad A(\Delta ADO)=A(\Delta BCO).\;\;\;\;\;\textcolor{#800000}{(iii)}[/tex]
Assim, temos que:
[tex]\qquad \qquad A(ABCD)=A(\Delta AOB)+A(\Delta BCO)+A(\Delta COD)+A(\Delta AOD)[/tex]
e da igualdade [tex]\textcolor{#800000}{(iii)}[/tex] concluímos que:
[tex]\qquad \qquad A(ABCD)=A(\Delta AOB)+2\cdot A(\Delta AOD)+A(\Delta COD).[/tex]
De [tex]\textcolor{#800000}{(ii)}[/tex] e [tex]\textcolor{#800000}{(i)}[/tex] obtemos
[tex]\qquad \qquad A(ABCD)=A(\Delta AOB)+2\cdot \dfrac{3}{5}A(\Delta AOB)+\bigg(\dfrac{3}{5}\bigg)^2A(\Delta AOB).[/tex]
[tex]\qquad \qquad A(ABCD)=A(\Delta AOB)\bigg(1+2\cdot \dfrac{3}{5}+\bigg(\dfrac{3}{5}\bigg)^2\bigg)[/tex]
[tex]\qquad \qquad A(ABCD)=A(\Delta AOB)\cdot \dfrac{64}{25}.[/tex]
Finalmente,
[tex]\qquad \qquad \fcolorbox{black}{#eee0e5}{$\dfrac{A(\Delta AOB)}{A(ABCD)}=\dfrac{25}{64}$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
