.Problema para ajudar na escola: Uma área colorida de um círculo

Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)

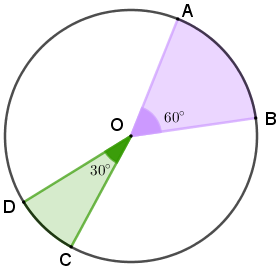
(XVIII OPM, 1999 – Adaptado) A área do círculo da figura abaixo mede [tex]40 \, cm^2.[/tex]
Se as medidas dos ângulos [tex]A\hat{O}B[/tex] e [tex]C\hat{O}D[/tex] são respectivamente [tex]60^\circ [/tex] e [tex]30^\circ[/tex], determine a medida da área colorida do círculo.

Solução 1

Podemos resolver este problema estabelecendo proporções entre “a área total do círculo” (o todo) e “cada região colorida” (as partes). O parâmetro que utilizaremos é a medida dos ângulos que definem as três regiões. As partes são definidas por ângulos de [tex]30^\circ [/tex] e [tex]60^\circ[/tex], de acordo com os dados do problema, e o todo é definido por um ângulo de [tex]360^\circ [/tex], uma volta completa.
Com base nessa proporção, determinaremos as medidas das respectivas áreas das duas regiões coloridas do círculo resolvendo duas regrinhas de três simples.

Área verde: [tex]\textcolor{#329865}{A_{v}}[/tex]

[tex]\begin{array}{c c c}
\qquad 40 \, cm^2 & \text{————–} & 360^\circ \qquad \\
\qquad \textcolor{#329865}{A_{v}} & \text{————–} & 30^\circ \qquad \end{array}[/tex]

Dessa forma, obtemos que
[tex]\quad \textcolor{#329865}{A_{v}} \times 360^\circ= 40 \times 30^\circ[/tex],
donde:
[tex]\quad \textcolor{#329865}{A_{v}} =\dfrac{ 40 \times 30}{360}=\dfrac{10}{3} \, cm^2[/tex].

Área lilás: [tex]\textcolor{#9A67C3}{A_l}[/tex]

[tex]\begin{array}{c c c}
\quad 40 \, cm^2 & \text{————–} & 360^\circ \qquad \\
\quad \textcolor{#9A67C3}{A_{l}} & \text{————–} & 60^\circ \qquad \end{array}[/tex]

Dessa forma, obtemos que
[tex]\quad \textcolor{#9A67C3}{A_l} \times 360^\circ= 40 \times 60^\circ[/tex],
donde:
[tex]\quad \textcolor{#9A67C3}{A_{l}} =\dfrac{ 40 \times 60}{360}=\dfrac{40}{6}=\dfrac{20}{3} \, cm^2[/tex].

Portanto, a medida da área [tex]S[/tex] da região colorida do círculo pode ser assim calculada:
[tex] \qquad \qquad S=\textcolor{#329865}{A_{v}} + \textcolor{#9A67C3}{A_l}=\dfrac{10}{3}+\dfrac{20}{3}=\dfrac{30}{3}= \, \fcolorbox{black}{#eee0e5}{$10 \, cm^2$} \, .[/tex]

Solução elaborada pelos Moderadores do Blog.

Solução 2

Podemos rotacionar as duas regiões coloridas em torno do centro [tex]O[/tex] do círculo, sem sobrepô-las, de modo a obter uma região que corresponde a um quarto do círculo, já que teríamos um setor circular de [tex]90^\circ.[/tex]
Assim, a medida da área [tex]S[/tex] da região colorida é dada por:
[tex] \qquad \qquad S=\dfrac{40}{4}= \, \fcolorbox{black}{#eee0e5}{$10 \, cm^2$} \, .[/tex]

Um applet para ajudar

Você pode rotacionar as duas regiões coloridas para obter uma região que corresponde a um quarto do círculo utilizando o applet abaixo.

Instruções:
(1) Espere o aplicativo carregar completamente.
(2) Para fazer a rotação da região colorida de verde, clique no ponto C, mantenha o mouse pressionado e faça o movimento.
(3) Para fazer a rotação da região colorida de lilás, clique no ponto A,mantenha o mouse pressionado e faça o movimento.
(4) Para retornar à posição inicial, clique no centro das setinhas circulares que aparecem no canto superior direito do aplicativo.

OBMEP_ srdg, criado com o GeoGebra

Solução elaborada pelos Moderadores do Blog.

Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo.
Você pode abrir o arquivo diretamente no seu navegador (Chrome, Edge, Firefox, Safari, entre outros), mas também pode utilizar o software gratuito Adobe Acrobat Reader.
Caso o dispositivo que você está utilizando não tenha o Acrobat Reader instalado, é só clicar AQUI para fazer o download adequado ao seu dispositivo.

Arquivo