✏ Link do problema para dispositivos da Apple.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
Determine qual é o menor número inteiro [tex]x[/tex] tal que [tex]\left|2-\dfrac{3}{x} \right| \leqslant 2.[/tex]
(Extraído do livro Matemática – Volume único: Gelson Iezzi e outros.)

Lembretes
Definição: Se [tex]A[/tex] é um número real, chamamos de "módulo de [tex]A[/tex]" ou "valor absoluto de [tex]A[/tex]" o número real denotado por [tex]|A|[/tex] e assim definido:
[tex]|A|= \begin {cases}A,\text{ se } A\geqslant 0\\
-A,\text{ se } A\lt 0 \end{cases}.[/tex]
Propriedades importantes: Sejam [tex]A[/tex] e [tex]B[/tex] números reais, com [tex]B \gt 0[/tex].
(1) [tex]|A|[/tex] é um número não negativo.
Em símbolos: [tex]|A|\geqslant 0.[/tex]
(2) A afirmação [tex]\boxed{\;|A|=B\;}[/tex] equivale à afirmação [tex]\;\boxed{A=B \,\text{ ou }\, A=-B\;}\,.[/tex]
Em símbolos: [tex]|A|=B\,\, \iff \; [/tex] [tex]A=B \, \, [/tex] ou [tex] \, \, A=-B.[/tex]
(3) A afirmação [tex]\boxed{\;|A|\lt B\;}[/tex] equivale à afirmação [tex]\;\boxed{-B \lt A \lt B\,}\;.[/tex]
Em símbolos: [tex]|A|\lt B\; \iff\; -B \lt A \lt B.[/tex]
(4) A afirmação [tex]\boxed{\;|A|\gt B\;}[/tex] equivale à afirmação [tex]\;\boxed{A \lt -B\,\text{ ou }\,A \gt B\;}\,.[/tex]
Em símbolos: [tex]|A|\gt B\; \iff\; A \lt -B[/tex] ou [tex]A \gt B.[/tex]
(5) A afirmação [tex]\boxed{\;|A|\leqslant B\;}[/tex] equivale à afirmação [tex]\;\boxed{-B \leqslant A \leqslant B\;}\,.[/tex]
Em símbolos: [tex]|A|\leqslant B \;\iff\; -B \leqslant A \leqslant B.[/tex]
(6) A afirmação [tex]\boxed{\;|A|\geqslant B \;}[/tex] equivale à afirmação [tex]\;\boxed{A \leqslant -B \,\text{ ou }\,A \geqslant B\;}\,.[/tex]
Em símbolos: [tex]|A|\geqslant B\; \iff\; A \leqslant -B[/tex] ou [tex]A \geqslant B.[/tex]
Solução
Pela propriedade (5) do Lembrete,
[tex]\left|2-\dfrac{3}{x} \right| \leqslant 2 \iff -2 \leqslant 2-\dfrac{3}{x} \leqslant 2.[/tex]
Assim, se [tex]x[/tex] é um número inteiro tal que [tex]\left|2-\dfrac{3}{x} \right| \leqslant 2[/tex], obtemos a seguinte sequência de desigualdades equivalentes:
[tex]\qquad -2 \leqslant 2-\dfrac{3}{x} \leqslant 2[/tex]
[tex]\qquad -2\textcolor{red}{-2} \leqslant 2-\dfrac{3}{x} \textcolor{red}{-2} \leqslant 2 \textcolor{red}{-2}[/tex]
[tex]\qquad -4 \leqslant \dfrac{-3}{x} \leqslant 0[/tex]
[tex]\qquad -4 \textcolor{red}{\cdot (-1) \geqslant} \dfrac{-3}{x} \textcolor{red}{\cdot (-1)\geqslant} 0\textcolor{red}{\cdot (-1)}[/tex]
[tex]\qquad 4 \geqslant \dfrac{3}{x} \geqslant 0. \qquad \textcolor{#800000}{(i)}[/tex]
De [tex]\textcolor{#800000}{(i)}[/tex], temos que [tex] 0 \leqslant \dfrac{3}{x} [/tex], o que nos garante que [tex] 0 \lt x. [/tex] ( Se [tex]x[/tex] fosse [tex]0[/tex], a fração [tex]\dfrac{3}{x}[/tex] não estaria definida, não é?)
Dessa forma, ainda de [tex]\textcolor{#800000}{(i)}[/tex], podemos concluir que, se [tex]x[/tex] é um número inteiro tal que [tex]\left|2-\dfrac{3}{x} \right| \leqslant 2[/tex], então:
[tex]\qquad x \geqslant \dfrac{3}{4}. \qquad \textcolor{#800000}{(ii)}[/tex]
Como no problema é solicitado o menor número inteiro [tex]x[/tex] tal que [tex]\left|2-\dfrac{3}{x} \right| \leqslant 2[/tex], segue de [tex]\textcolor{#800000}{(ii)}[/tex] que [tex] \, \fcolorbox{black}{#eee0e5}{$x=1$} \, .[/tex] ( Veja o esqueminha abaixo)
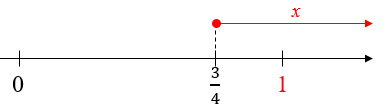
Vocês podem visualizar geometricamente essa solução traçando o gráfico da função definida por [tex]\textcolor{blue}{f(x)=\left|2-\dfrac{3}{x} \right|}[/tex] e da reta [tex]\textcolor{#009900}{y=2}[/tex] em um mesmo plano cartesiano, conforme ilustra a figura a seguir.
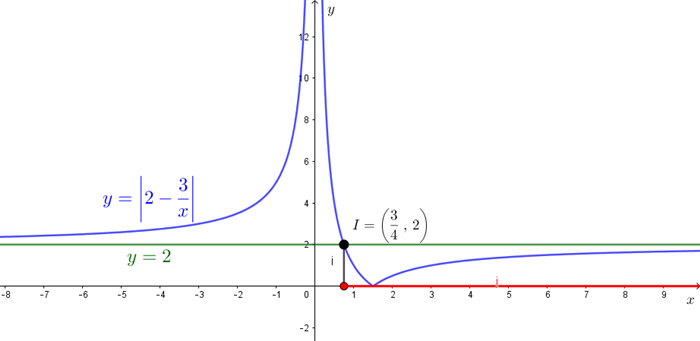
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
